Aufgabe:
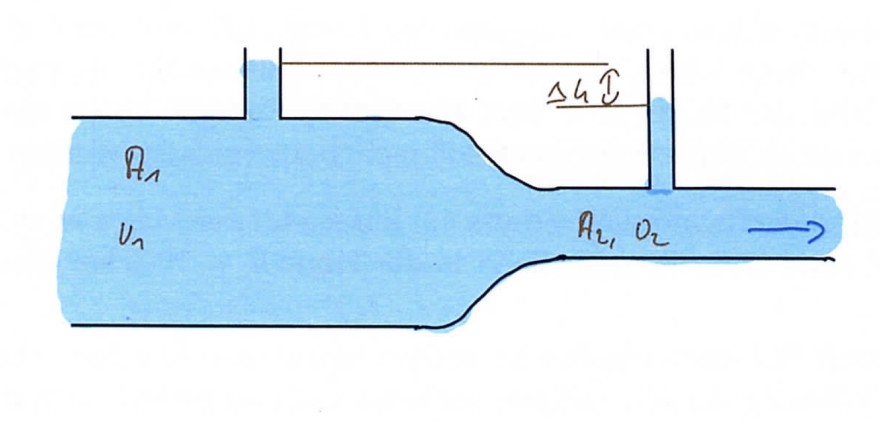
Durch ein horizontal verlaufendes Rohr mit ungleichen Querschnitten A1 = 2*10-3m2 und A2 = 1*10-3m2 strömt Wasser mit der Geschwindigkeit v1 bzw. v2. Es ist der Volumenstrom durch das Rohr zu ermitteln, wenn die beiden Schenkel der Flüssigkeitsmanometer eine Höhendifferenz von △h=0,2 m zeigen.
Problem/Ansatz:
Ich habe damit angefangen die Bernoulli-Gleichung aufzustellen. Diese lautet:
$$p_1+\frac{\rho}{2}v_1^2=p_2+\frac{\rho}{2}v_2^2$$
und umgestellt...
$$p_1-p_2=\frac{\rho}{2}v_2^2-\frac{\rho}{2}v_1^2=\Delta p$$
$$\frac{\rho}{2}v_2^2-\frac{\rho}{2}v_1^2 = \rho gh$$
$$\frac{v_2^2}{2}-\frac{v_1^2}{2}=gh$$
$$v_2=\sqrt{2gh}+v_1$$
Dann mit der Kontinuitätsgleichung das Verhältnis zwischen den Geschwindigkeiten ermittelt:
$$v_1*A_1=v_2*A_2$$
$$\frac{v_1}{v_2}=\frac{A_2}{A_1} = 0.5$$
bedeutet, v1 ist halb so groß wie v2: v1 = v; v2 = 2v
$$\rightarrow v_2=\sqrt{2gh}+v_1$$
$$2v=\sqrt{2gh}+v$$
$$v=\sqrt{2gh}$$
$$\rightarrow v_1=v=\sqrt{2gh}$$
Für den Volumenstrom ergibt sich damit:
$$\dot{V}=v_1*A_1 ≈ 0.004\frac{m^3}{s}$$
Ich wollte einmal fragen, ob das ganze richtig ist.