Aufgabe:
Problem/Ansatz:
Text erkannt:
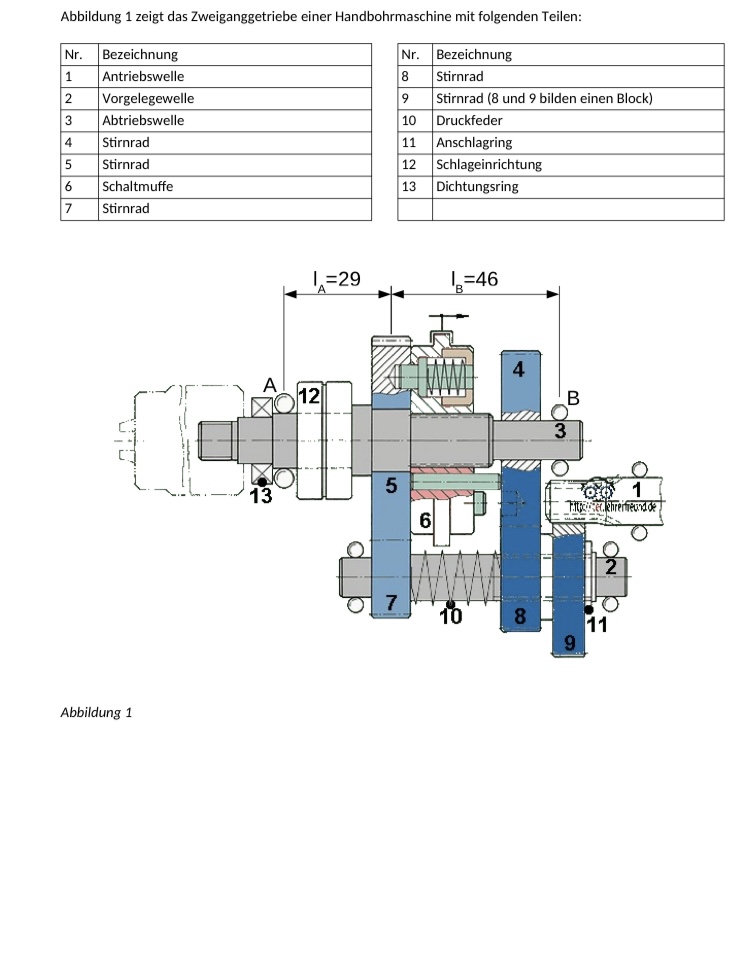
Abbildung 1 zeigt das Zweiganggetriebe einer Handbohrmaschine mit folgenden Teilen:
\begin{tabular}{|l|l|}
\hline \( \mathrm{Nr} \). & Bezeichnung \\
\hline 1 & Antriebswelle \\
\hline 2 & Vorgelegewelle \\
\hline 3 & Abtriebswelle \\
\hline 4 & Stirnrad \\
\hline 5 & Stirnrad \\
\hline 6 & Schaltmuffe \\
\hline 7 & Stirnrad \\
\hline
\end{tabular}
\begin{tabular}{|l|l|}
\hline Nr. & Bezeichnung \\
\hline 8 & Stirnrad \\
\hline 9 & Stirnrad (8 und 9 bilden einen Block) \\
\hline 10 & Druckfeder \\
\hline 11 & Anschlagring \\
\hline 12 & Schlageinrichtung \\
\hline 13 & Dichtungsring \\
\hline & \\
\hline
\end{tabular}
Abbildung 1

Text erkannt:
Arbeitsblatt
Name:
S.2/2
1 Zeichne in Abbildung 2 die Kraftflüsse des langsamen und des schnellen Gangs mit verschiedenen Farben ein.
Abbildung 2
2 Beschreibe die Abläufe der Kraftflüsse im langsamen Gang. Beschreibe den Schaltvorgang in den schnellen Gang. Beachte dabei auch die Funktion des Bolzens und der Feder in der Schaltmuffe.
Hinweis: Der Kraftfluss ist der gedankliche Verlauf von Kräften in Baugruppen. Krafteinleitungsstellen sind die Punkte, an denen Kräfte von außen ein Bauteil belasten. Lager übertragen die Kräfte an Nachbarbauteile.
3 Die Motorwelle dreht mit \( 1500 \mathrm{~min}^{-1} \). Die Antriebsleistung beträgt \( 1200 \mathrm{~W} \).
Die Räder 1 und 9 sind mit dem Modul \( m=1 \mathrm{~mm} \) verzahnt.
Die Räder 8 - 4 und 7 - 5 sind mit dem Modul \( m=1,5 \mathrm{~mm} \) verzahnt.
\( \mathrm{z}_{1}=9 ; \mathrm{z}_{9}=30 ; \mathrm{z}_{\mathrm{B}}=35 ; \mathrm{z}_{7}=26 ; \mathrm{z}_{4}=57 ; \mathrm{z}_{5}= \) ?
3.1 Berechne die Achsabstände \( a_{1} \) zwischen den Wellen 1 und 2 bzw. \( a_{2} \) zwischen den Wellen 2 und 3.
3.2 Ermittle die Zähnezahl des Zahnrads 5.
3.3 Berechne die Gesamtübersetzungsverhältnisse in beiden Gängen. Ermittle die Drehzahlen der Bohrspindel im langsamen und schnellen Gang.
3.4 Berechne die Zahnkraft (Umfangskraft) am Zahnrad 4 im schnellen Gang. Berechne das Drehmoment, das durch die Schaltmuffe auf die Abtriebswelle übertragen wird.
3.5 Ermittle
3.5.1 die an den Wellen 1, 2 und 3 wirkenden Drehmomente.
3.5.2 die in A und B wirkenden Lagerkräfte. Vernachlässige dabei den Zahn-Eingriffswinkel.

Text erkannt:
3. 1
Achsabstand \( a_{1} \)
\( \begin{aligned} m_{1} & =1 \mathrm{~mm} \\ z_{1} & =9 \\ z_{9} & =30 \\ a_{1} & =m_{1} \frac{\left(z_{1}+z_{9}\right)}{\bar{c}} \\ & =1 \mathrm{~mm} \frac{(9+30)}{2}=19,5 \mathrm{~mm} \\ \text { dito } a_{2} & =69 \mathrm{~mm} \end{aligned} \)
\( \begin{array}{l} a_{1}=195 \mathrm{~mm} \\ a_{2}=69 \mathrm{~mm} \\ z_{5}=66 \\ i_{S}=5,43 \text { sclunll } \\ i_{L}=8,15 \text { langsam } \\ n_{L}=184,05 \mathrm{~min}^{-1} \\ n_{S}=276,24 \mathrm{~min}^{-1} \end{array} \)
3.2
\( \begin{array}{l} \left.a_{2}=m_{2} \frac{\left(z_{5}+z_{7}\right)}{2} \right\rvert\, \cdot m_{2} \\ \left.\frac{a_{2}}{m_{2}}=z_{5}+z_{7} \right\rvert\,-z_{7} \\ \frac{a_{2}}{m_{2}}-z_{7}=z_{5} \\ =\frac{69 \mathrm{~mm}}{1,5 \mathrm{~mm}}-26=66 \end{array} \)
3.3
Srhnell \( i_{s}=\frac{z_{9} \cdot z_{4}}{z_{1} \cdot z_{8}}=\frac{30 \cdot 57}{9 \cdot 35}=5,429 \)
dito
Langsam \( i_{L}=\frac{z_{9} \cdot z_{5}}{z_{n} \cdot z_{7}}=\frac{30 \cdot 66}{9 \cdot 26}=8,462 \)
\( \begin{array}{l} n_{s}=\frac{n_{e}}{i_{c}}=\frac{1500 \mathrm{~min}^{-1}}{5,429}=276,29 \mathrm{~min}^{-1} \\ n_{L}=\frac{n_{e}}{i_{s}}=\frac{1500 \mathrm{~min}^{-1}}{8,462}=177,26 \mathrm{~min}^{-1} \end{array} \)

Text erkannt:
3.4
\( M_{1}=\frac{p \cdot 9550}{n}=\frac{1,2 \cdot 9550}{1500}=7,64 \mathrm{Vm} \)
Eingangsmoment
\( \begin{aligned} M_{4}=i_{5} \cdot M_{1} & =5,429 \cdot 7,64 \mathrm{Nm} \\ & =41,48 \mathrm{Nm} \end{aligned} \)
\( \begin{array}{r} d_{4}=m_{2} \cdot z_{4}=1,5 \mathrm{~mm} \cdot 57=85,5 \mathrm{~mm} \\ \Rightarrow v_{4}=42,75 \mathrm{~mm} \\ M_{4}=F_{4} \cdot v_{4} \\ \frac{M_{4}}{r_{4}}=\frac{41,48 \mathrm{Nm}}{0,04275 \mathrm{~m}}=970,3 \mathrm{~N} \end{array} \)
3.5.1
\( \begin{array}{l} M_{1}=7,64 \mathrm{Nm} \\ M_{35}=41,48 \mathrm{Nm} \\ M_{2}=M_{1} \cdot i_{1}=7,64 \mathrm{Nm} \cdot \frac{30}{9}=25,47 \mathrm{Nm} \\ M_{3 L}=M_{1} \cdot i_{l}=7,66 \mathrm{Nm} \cdot 8,46=64,63 \mathrm{Nm} \end{array} \)