Könnte bitte jemand bei „e“ helfen. Verstehe nicht ganz, wie man mit der Phase multiplizieren kann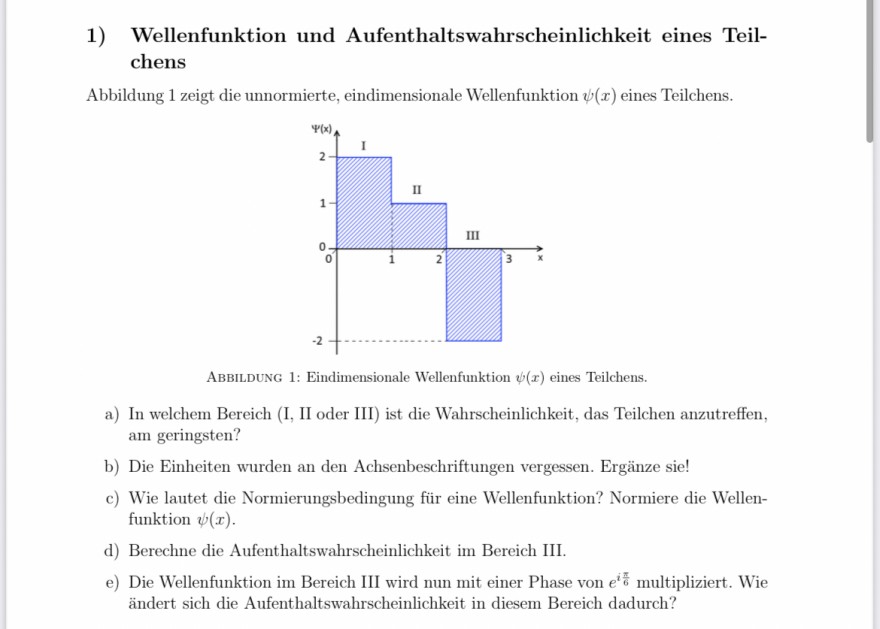
Text erkannt:
1) Wellenfunktion und Aufenthaltswahrscheinlichkeit eines Teilchens
Abbildung 1 zeigt die unnormierte, eindimensionale Wellenfunktion \( \psi(x) \) eines Teilchens.
AbBildung 1: Eindimensionale Wellenfunktion \( \psi(x) \) eines Teilchens.
a) In welchem Bereich (I, II oder III) ist die Wahrscheinlichkeit, das Teilchen anzutreffen, am geringsten?
b) Die Einheiten wurden an den Achsenbeschriftungen vergessen. Ergänze sie!
c) Wie lautet die Normierungsbedingung für eine Wellenfunktion? Normiere die Wellenfunktion \( \psi(x) \).
d) Berechne die Aufenthaltswahrscheinlichkeit im Bereich III.
e) Die Wellenfunktion im Bereich III wird nun mit einer Phase von \( e^{i \frac{\pi}{6}} \) multipliziert. Wie ändert sich die Aufenthaltswahrscheinlichkeit in diesem Bereich dadurch?

Text erkannt:
a) Im Berercu II
die Flache der Welleafunkrrou an gerrengstom d. h. dass dre WF se|pst and \( |\psi| x||^{2} \) wech an yeriagsten
bा
\( \begin{aligned} \int \limits_{-4}^{\infty}|\psi(x)|^{2} u x & =1 \\ x & =1 m \end{aligned} \)
awhant
\( \begin{array}{l} |Y(x)|^{2}=\frac{1}{d t}=\frac{1}{m} \\ \Psi(x)=\sqrt{\frac{1}{m}} \end{array} \)
oder \( \sum \limits_{\Delta x}|A \cdot \Psi(x)|^{2} \Delta x=1 \)
\( \begin{array}{l} A: i^{2} \cdot\left[(2 \cdot 1)^{2}+\left(1 \cdot(1)^{2}+|-2 \cdot 1|^{2}\right)^{3}\right]=1 \\ A 3^{2}[4+1+4]=A^{2} \cdot S=1 \\ A=\frac{1}{3} \\ \end{array} \)
d) \( \pi: \sum\left|Y^{n}(\Delta x)\right|^{2} \Delta^{x} \Leftrightarrow \)
III: \( \sum \psi^{n}(\Delta x) \) im Berercu III \( \cdots 1=\frac{2}{3} \)
\( \Leftrightarrow\left|-\frac{2}{3}\right|^{2} \cdot 1=\frac{u}{9}=04 \overline{4} \)
Text erkannt:
(1)
a) Im Bererm II
die Flacke der Welleatunktron an gerrengstom 1. h. dass die WF selpst and \( \mid \) Wat \( \|^{2} \) areca an geriagsten
bi
\( \begin{aligned} \int \limits_{-4}|\psi(x)|^{2} u x & =1 \\ x & =1 m \end{aligned} \)
whant
\( \begin{array}{l} |Y(x)|^{2}=\frac{1}{a x}=\frac{1}{m} \\ \psi(x)=\sqrt{\frac{1}{m}} \end{array} \)
\( \operatorname{oder} \sum \limits_{\Delta x}|A \cdot \Psi(x)|^{2} \Delta x=1 \)
\( \begin{array}{l} \left.A i^{2} \cdot\left[(12 \cdot 1)^{2}+\left(1 \cdot||^{2}+\mid-2 \cdot 1\right)^{2}\right)^{3}\right]=1 \\ A 3^{\prime}[4+1+4]=A^{2} \cdot 9=1 \\ A=\frac{1}{3} \\ \end{array} \)
d) \( \pi: \sum 1 \)
\( \begin{array}{l} \text { III: } \frac{\sum\left|Y^{n}(\Delta x)\right|^{2} \Delta x}{\psi^{n}(\Delta x) \text { im Bererc III }} \ldots \\ \Rightarrow\left|-\frac{2}{3}\right|^{2} \cdot 1=\frac{u}{9}=04 \frac{2}{3} \end{array} \)
\( 1 \)
