Aufgabe:
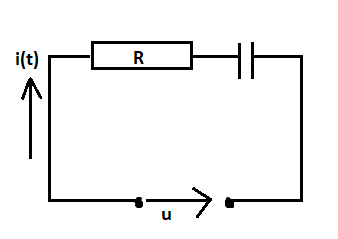
C steht für den Kondensator
R ist ohmscher Widerstand
U_c ist Kondensatorspannung
U ist außen angelegt
$$R*C*\frac{d_Uc}{dt} + U_C = U$$
a)
1) U = const
2) AWP U_c(0) = 0
b) dasselbe für die Werte:
R= 1000Ω; C= 10µF
Problem/Ansatz:
a) 1)$$R*C*\frac{d_Uc}{dt} + U_C = U$$
$$R*C*\frac{d_Uc}{dt} + U_C = 0$$
Uh = K*e(-1/RC) *t
Up = U; U'p = 0
R*C*0+ Up = U
Up = U
U = Uh + Up = K*e(-1/RC) *t + U
2) U_c(0) = 0 <=> K*e0 + U = 0 <=> K+ U = 0 => K= -U
Randbedingung eingesetzt in U(t) : U(t) = -U*e(-1/RC)*t + U
b) R= 1000Ω; C= 10µF= 1*10-5 F
1000Ω* 1*10-5F * \( \frac{d_Uc}{dt} \) + U_c = 400 V (da ist auch mit U_c wie in a) die Spannung des Kondensators gemeint, keine separate Einheit)
0,01s * U'_c + U_c = 400V
Uh = K*e(-1/0,01[s])*t
Up = 400 V U'p = 0
0,01s*0 + 400V = 400 V
400 V = 400 V [komme da leider nicht weiter bzw. verstehe nicht wie man daraus ableitet Up= 400 V
[a = 400V
U_p = 400V]