Aufgabe:
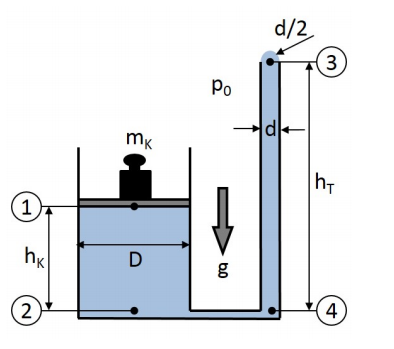
Zur Messung der Oberflächenspannung \( \sigma \) einer Flüssigkeit soll die in der Skizze gezeigte U-Rohr-Anordnung
verwendet werden: Im linken Schenkel wird die Masse eines Kolbens mit Durchmesser D solange bis zum Wert
\( m_{K} \) erhöht bis am oberen Ende des rechten Schenkels ein Tropfen mit dem Radius d/2 entsteht.
Die Flüssigkeit
ist inkompressibel und hat die Dichte \( \rho . \) Der Umgebungsdruck beträgt \( p_{0}, \) die Gravitationsbeschleunigung g.
Was gilt für die Drücke \( p_{1} \) und \( p_{2} \) an den markierten Stellen (1) und (2)?
\( [\quad]\ p_{1}=p_{0}+\frac{g m_{K}}{\pi D^{2}} \)
\( [\quad]\ p_{1}=p_{0} \)
\( [ x ]\ p_{1}=p_{1}=p_{0}+\frac{4 g m_{K}}{\pi D^{2}} \)
\( [\quad]\ p_{2}=\frac{4 g m_{K}}{\pi D^{2}}+\rho g h_{K} \)
\( [x]\ p_{2}=p_{0}+\frac{4 g m_{K}}{\pi D^{2}}+\rho g h_{K} \)
\( [\quad]\ p_{2}=p_{0}+\frac{g m_{K}}{\pi D^{2}}+\rho g h_{T} \)
Was gilt für die Drücke \( p_{3} \) und \( p_{4} \) an den markierten Stellen (3) und (4)?
\( [\quad] p_{3}=p_{0} \)
\( [x] p_{3}=p_{0}+\frac{4 \sigma}{d} \)
\( [\quad] p_{3}=p_{0}-\frac{4 \sigma}{d} \)
\( [\quad] p_{4}=p_{0}+\frac{4 \sigma}{d}+\rho g h_{T} \)
\( [x] p_{4}=p_{0}+\frac{4 \sigma}{d}+\rho g h_{K} \)
\( [\quad] p_{4}=p_{0}-\frac{4 \sigma}{d}+\rho g h_{T} \)
Wie groß ist die Oberflächenspannung \( \sigma \) der Flüssigkeit?
\( [\quad] \sigma=g d\left(\frac{m K}{\pi D^{2}}+\frac{\rho}{4}\left(h_{K}-h_{T}\right)\right) \)
\( [\quad] \sigma=g d \frac{ρ}{4}\left(h_{K}-h_{T}\right) \)
\( [\quad] \sigma=g d \frac{m K}{\pi D^{2}} \)
\( [\quad] \sigma=g d\left(\frac{m_{K}}{\pi D^{2}}+\frac{\rho}{4}\left(h_{T}-h_{K}\right)\right) \)
\( [x] \sigma=\frac{1}{g d}\left(\frac{m_{K}}{\pi D^{2}}+\frac{\rho}{4}\left(h_{K}-h_{T}\right)\right) \)
\( [\quad] \frac{1}{g d}\left(\frac{\pi D^{2}}{m_{K}}+\frac{\rho}{4}\left(h_{K}-h_{T}\right)\right) \)
Sind meine angekreuzten Ergebnisse richtig?