welche Formel muss ich hier anwenden?
Volumenarbeit:
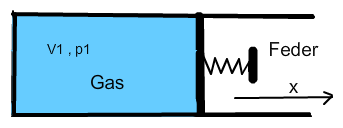
Ein ideales Gas mit Volumen V1 und Druck p1 wird durch einen Kolben mit der Querschnittsfläche A zusammengedrückt. Der Druck auf den Kolben wird über eine (lineare) Feder mit der Federkonstante k ausgeübt.
a) um welche Strecke x1 ist die Feder in diesem Zustand gestaucht?
b) Das Gas wird (langsam, ohne Reibungsverluste) erhitzt, bis sich das Volumen auf den Wert V2 erhöht. Berechne die verrichtete Arbeit W1-2 des Gases an der Feder.
Der äußere Luftdruck soll in beiden Aufgaben vernachlässigt werden.
Gruß