Hallo Fridolin,
Ich werde nur nicht so ganz schlau raus, wie ich die "Wippe" betrachten soll.
Zum Bespiel so:
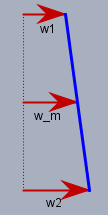
Bewegt sich das obere Ende der Wippe um \(w_1\) nach rechts und das untere Ende um \(w_2\) so muss sich die Mitte bei einer starren Wippe um $$\frac12(w_1+w_2) = w_m$$ nach rechts bewegen. Das untere Ende aus der Aufgabe wird um \(\Delta l_T\) auf Grund des Temperaturanstiegs verlängert und um \(\Delta l_{St}\) wieder zusammen gedrückt, also ist \(w_2 = \Delta l_T - \Delta l_{St}\). Das obere Ende wird nur um \(\Delta l_{Al}\) zusammen gedrückt (\(w_1 = -\Delta l_{Al}\)) und die Mitte soll sich um \(w_m=\Delta l_{Cu}\) nach rechts bewegen. Folglich ist dann $$\frac12(\Delta l_{T} - \Delta l_{St} - \Delta l_{Al}) = \Delta l_{Cu} \quad (1) $$ Berechne nun die Federkonstanten \(D\) der einzelenen Stäbe nach \(\displaystyle D=\frac{E \cdot A}{l_0}\). Beim Aluminiumstab gilt es die 'Reihenschaltung' zu beachten. Auf Grund des Momenten- und Kräftegleichgewichts sind die Kräfte im Stahl und im Aluminium gleich groß und beide halb so groß wie die Kraft im Kupferstab. D.h.: $$\begin{aligned} D_{Al} \cdot \Delta l_{Al} &= D_{St} \cdot \Delta l_{St} \quad &(2)\\ D_{Al} \cdot \Delta l_{Al} &= \frac12 D_{Cu} \cdot \Delta l_{Cu} \quad &(3)\end{aligned}$$ Somit liegen drei Gleichungen (1), (2) und (3) für die drei unbekannten Längenänderungen \(\Delta l\) vor.
Sollte noch etwas unklar sein, so frage bitte nach.