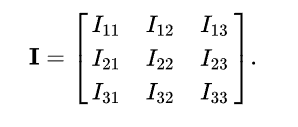
Text erkannt:
\( \mathbf{I}=\left[\begin{array}{lll}I_{11} & I_{12} & I_{13} \\ I_{21} & I_{22} & I_{23} \\ I_{31} & I_{32} & I_{33}\end{array}\right] \)
1) Also wir haben jetzt z.B. ein Koordinatensystem mit drei Achsen. Jede dieser Achsen hat einen Trägheitsmoment, z.B. hat jetzt die x-Achse einen Trägheitsmoment von (I_11, I_12, I_13). Wenn z.B. ein Körper der sein Zentrum der Masse im Ursprung dieses Koordinatensystems hat, und man rotiert den Körper um die x-Achse, dann wäre (I_11, I_22, I_13) quasi das äquivalent der Masse bei der Rotation.
2)Wenn wir jetzt aber z.B. ein anderes Koordinatensystem wählen, dann hätten die Achsen von diesem auch vermutlich andere Trägheitsmomente. Man könnte dann z.B. wenn man ein lokales Koordinatensystem hat einen Tensor I_lokal definieren.
Ich hoffe, das ist so verständlich – ich bin mir bei dem Thema selbst noch etwas unsicher. Falls ich irgendwo falsch liege, gerne korrigieren!