Schaltvorgang im Netzwerk mit Kondensator

Question

Aufgabe:

Zum Zeitpunkt t=0 ist der Schalter geschlossen.

Berechne den Zeitverlauf für U₂(t) für t>=0.

Verwende U₂(-0) und U₂(∞) und gebe die Zeitkonstante T des Ladevorgangs an.

Text erkannt:

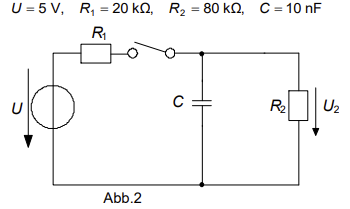
\( U=5 \mathrm{~V}, \quad R_{1}=20 \mathrm{k} \Omega, \quad R_{2}=80 \mathrm{k} \Omega, \quad C=10 \mathrm{nF} \)
Abb.2

Mein Ansatz:

Folgende Rechnung habe ich durchgeführt:

1. Ersatzspannungsquelle: U_q = U * (R2/(R1+R2)) = 4V

2. Innenwiderstand: Ri = (R1*R2) / (R1+R2) = 16k Ohm

3. Zeitkonstante T= Ri * C = 0,16ms

4. Spannungsfunktion: U₂(t)= (U₂(-0) - U₂(∞) * e^-(t/T)+ U₂(∞) = -4V * e^-(t/0,16ms) + 4V

Habe ich mit meinem Vorgehen die Aufgabe korrekt gelöst oder fallen euch Fehler auf?

Comments

für was soll denn der Innenwiderstand sein?

und 4V ist die Spannung an R2 für t=oo

bei t=0 ist U2=0 weil C wie ein Kurzschluss wirkt, bzw

Uc=U2 in jedem Moment.

musst du nicht die Dgl für den Prozess aufstellen ?

---

Ich soll ja die Zeitkonstante berechnen und die ist mit T = R * C definiert. Um mein R zu erhalten muss ich doch zunächst die Ersatzspannungsquelle und den Innenwiderstand bilden.

Anschließend kann ich die Zeitkonstante für den Kondensator errechnen und damit Spannungsverlauf von U₂ , da dieser identisch wie Uc verläuft.

Welche Dgl meinst du ?

Etwa U₂ = U_q * (1- e^-(t/T)) ?

Beschreibt U2(t)= (U2(-0) - U2(∞) * e-(t/T)+ U2(∞) etwa nicht den gleichen Spannungsverlauf?

Grüße

Answer 1

in meinen Augen gelöst wie ein Profi. Der stellt keine Differentialgleichung auf, sondern rechnet genau so, wie du es gemacht hast. Nur ein kleiner Schreibfehler: es fehlt eine Klammer ... ))*e...