Der Vergleich mit der Kraft ist gut, du musst aber die Fläche als die Kraft ansehen und den Abstand des Schwerpunktes von der Linie AE als Wirkungslinie.
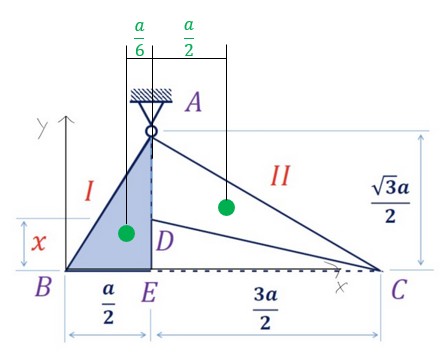
Für das Dreieck I liegt der Schwerpunkt auf 1/3 der Linie BE von der Linie AE entfernt. BE ist a/2 lang. Der Abstand ist also a/6.
Für das Dreieck II liegt der Schwerpunkt 1/3 der Linie EC von der Linie AE entfernt. EC ist 3a/2 lang. Der Abstand ist also a/2.
Das Dreieck II hat mit seiner Schwerpunktlage eine dreimal größere Wirkungslinie, also muss das Dreieck II flächenmäßig dreimal kleiner sein als Dreieck I.
Mein Ergebnis ist \(x=a\frac{4}{9}\sqrt{3}\)
das musst du aber noch einmal nachrechnen. Ich hätte erwarte, dass das \(\sqrt{3}\) sich auflöst.