Text erkannt:
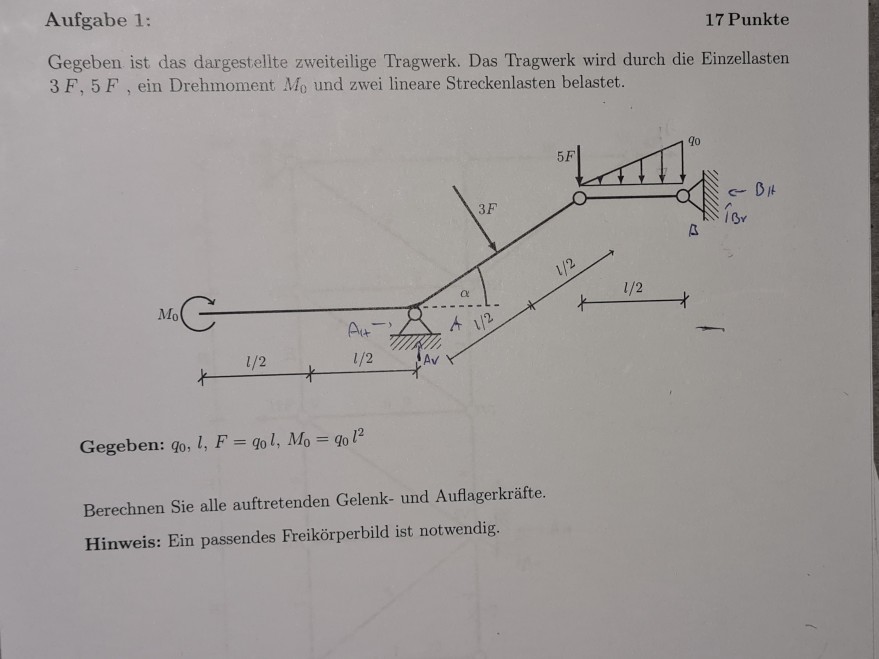
Aufgabe 1:
17 Punkte
Gegeben ist das dargestellte zweiteilige Tragwerk. Das Tragwerk wird durch die Einzellasten \( 3 F, 5 F \), ein Drehmoment \( M_{0} \) und zwei lineare Streckenlasten belastet.
Gegeben: \( q_{0}, l, F=q_{0} l, M_{0}=q_{0} l^{2} \)
Berechnen Sie alle auftretenden Gelenk- und Auflagerkräfte.
Hinweis: Ein passendes Freikörperbild ist notwendig.
Aufgabe:
Hallo,
ich habe hier eine Aufgabe aus der Mechanik, wo ich die Auflager- und Gelenkkräfte berechnen muss. Nun ist es aber so, dass direkt auf das Gelenk eine Kraft wirkt. Wenn ich dann durchschneide ist die Kraft ja logischerweise auf eine der Seiten. Nun ist es aber so, dass ich, wenn die Kraft auf der anderen Seite ist andere Werte rausbekomme, als wenn sie auf der Seite ist, wo ich die Kräfte berechne ist. Ich weiß nicht, ob ich was falsch mache, oder ob das sich dann irgendwie durch das andere Teilsystem ausgleicht, soweit habe ich nicht gerechnet, aber selbst das würde in meinen Augen keinen Sinn machen.