Hallo ihr lieben, ich habe wieder Probleme bei der Berechnung des Massenträgheitsmoment:
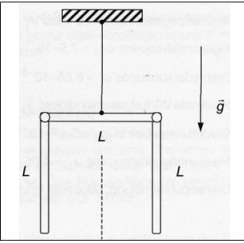
$$ \begin{array}{l}{\text { Physikalisches Pendel: Drei gleiche, dünne Stäbe }(\ell=30 \mathrm{cm},} \\ {m=0,2 \mathrm{kg} \text { ) bilden mit zwei (masselosen) steifen Gelenken ein }} \\ {\text { rechtwinkliges U. Der mittlere Stab ist in horizontaler Lage in }} \\ {\text { seinem Schwerpunkt an einem vertikalen torsionselastischen }} \\ {\text { Draht aufgehängt. Die beiden äußeren Stäbe hängen parallel }} \\ {\text { zum Torsionsdraht senkrecht nach unten. }}\end{array} $$
$$ \begin{array}{l}{\text { a) Berechnen Sie das Massenträgheitsmoment J der Stabanord- }} \\ {\text { nung für eine mit dem Draht zusammenfallende Dreh- und }} \\ {\text { Symmetrieachse (für einen dünnen Stab gilt bzgl. einer zur }} \\ {\text { Stabachse senkrechten Schwerpunktachse } J_{S}=\frac{1}{12} m l^{2} )}\end{array} $$
Lösung:
$$ J=10,5 \cdot 10^{-3} \mathrm{kgm}^{2} $$
Mein Ansatz
