Wahrscheinlichkeitsrechnung eines Stromkreises

Question

Es gibt drei Bauteile, alle haben dieselbe Wahrscheinlich von p, dass sie ausfallen.

Der Stromkreis besteht aus: Parallelschaltung von zwei solcher Bauteile, in Serie dann mit dem dritten.

Frage: Wie hoch ist die Wahrscheinlichkeit r, dass beim Einschalten der Stromkreis unterbrochen wird (ausgedrückt durch p)?

Comments

Mein Ansatz ist folgender.

Damit Strom fließt, muss das Bauteil ok sein, also (1-p).

Nach dem Baumdiagramm hätte ich Weg 1 + Weg 2 für Wahrscheinlichkeit, dass Strom fließt.

Da alle Bauteile eh gleich sind = 2 * Weg = 2 * (1-p)*(1-p).

Am Ende 1 - das.

Aber anscheinend stimmt es nicht.

---

Zuerst betrachten wir die Parallelschaltung:

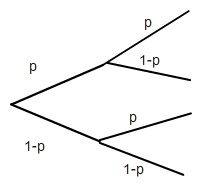
Wenn beide Bauteile kaputt sind, ist das der Pfad p*p=p².

Solange nur ein Bauteil kaputt ist oder beide ganz fließt der Strom. Hierfür ist die Wahrscheinlichkeit

p*(1-p)+(1-p)*p+(1-p)² = 2p-2p²+1-2p+p² = 1-p² (plausibel, weil das die Gegenwahrscheinlichkeit zu p² ist)

Jetzt reduzieren wird das Bild auf Strom fließt und Strom fließt nicht in der Parallelschaltung:

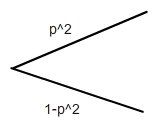
Ausgehend von der Parallelschaltung kommt jetzt die Reihenschaltung dahinter:

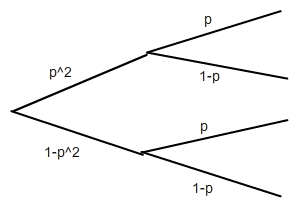
Wenn der Strom in der Parallelschaltung nicht durchkommt ist es egal was dahinterkommt, d.h. der obere Zweig beschränkt sich auf p². Beim unteren Zweig kommt der Strom nicht durch, wenn das dritte Bauteil versagt. Die Wahrscheinlichkeit hierfür ist: (1-p²)*p = p - p³.

Rechnet man die Wahrscheinlichkeiten dafür das der Strom in der Parallelschaltung nicht durchkommt (p²) und dass er beim dritten Bauteil nicht durchkommt (p-p³) zusammen, erhält man:

p + p² - p³

Answer 1

Die Wahrscheinlichkeit, dass die beiden parallel geschalteten Bauteile gleichzeitig ausfallen, beträgt p².

Somit ist die Wahrscheinlichkeit dafür, dass die Parallelschaltung oder das in Reihe geschaltete dritte Bauteil ausfallen:

p + p² - p³.

Dieses ist die gesuchte Wahrscheinlichkeit, dass der Stromkreis unterbrochen ist.

Comments

Du hast oben versucht, mit Hilfe des Baumdiagrammes die Wahrscheinlichkeit für einen Stromfluss zu bestimmen.

Gehen wir mal alle möglichen Pfade durch:

Pfad_1: Bauteil_3 ist nicht defekt (1 - p) und Bauteil_1 ist nicht defekt (1 - p)

P₁ = (1 - p)*(1 - p)

Pfad_2: Bauteil_3 ist nicht defekt (1 - p), Bauteil_1 ist defekt (p) und Bauteil_2 ist nicht defekt (1 - p)

P₂ = (1 - p)*p*(1 - p)

Bildet man die Summe und zieht diese von 1 ab, erhält man das obige Ergebnis:

1 - (P₁ + P₂) = p + p² - p³

Dein Fehler war, dass du den Weg 2 falsch bestimmt hast.

Answer 2

Unterbrechung, wenn A  oder (B und C) unterbrochen wird
$$U= A \lor (B \land C)$$

Eine Wertetabelle wäre der kunstloseste, aber hier noch gangbare Weg ...

Comments

Die umfangreichen Erläuterungen von Kommentator 1  hätten mich eigentlich überzeugt, wenn bei mir Unklarheiten bestanden hätten:

" Zuerst betrachten wir die Parallelschaltung:

Solange nur ein Bauteil kaputt ist oder beide ganz fließt der Strom. "

Was wird durch die Großbuchstaben klarer?