man findet hier viele seiner Komilitonen :D (hast du zufälligerweise die 4.1?)
also mein Vorschlag wäre (kann nicht garantieren das es richtig ist)
Skizze)
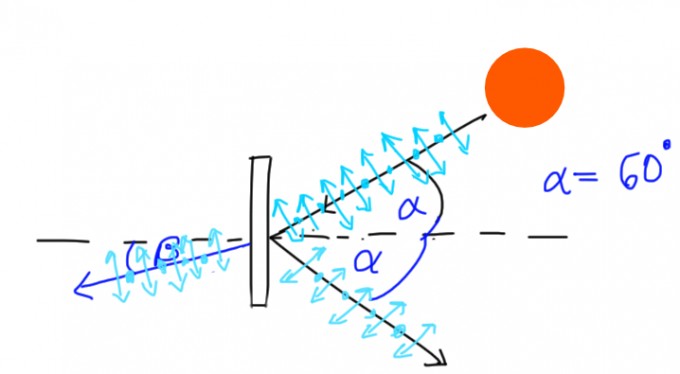
(1) erstmals ermitteln wir β mit:
$$ \beta=\arcsin(\frac{{n}_{L}\cdot \sin(\alpha)}{{n}_{G}}) $$
$$ \Rightarrow \beta=\arcsin(\frac{1.00\cdot \sin(60.0\deg)}{1.52})\approx 34.7\deg $$
(2.1) Jetzt gibt es ja im Skript die Formeln für die Reflexionskoeffizienten, also für die p-Polarisation gilt:
$${r}_{p}=\frac{ {n}_{2}\cdot \cos(\alpha) - {n}_{1}\cdot \cos(\beta) }{ {n}_{2}\cdot \cos(\alpha) + {n}_{1}\cdot \cos(\beta) }$$
$$\Rightarrow {r}_{p}=\frac{ 1.52\cdot \cos(60.0\deg) - 1\cdot \cos(34.7\deg) }{ 1.52\cdot \cos(60.0\deg) + 1\cdot \cos(34.7\deg) } \approx -0.0393$$
(2.2) für die s-Polarisation gilt:
$${r}_{s}=\frac{ {n}_{1}\cdot \cos(\alpha) - {n}_{2}\cdot \cos(\beta) }{ {n}_{1}\cdot \cos(\alpha) + {n}_{2}\cdot \cos(\beta) }$$
$$\Rightarrow {r}_{s}=\frac{ \cos(60.0\deg) - 1.52\cdot \cos(34.7\deg) }{ \cos(60.0\deg) + 1.52\cdot \cos(34.7\deg) } \approx -0.428$$
(3) Daraus folgen die p-s Reflexionsgradien [die p bzw. s-Polarisationsanteile im reflektierenden Strahl]:
$${R}_{p} = {( \frac{{I}_{r}}{{I}_{0}}) }_{p} = {{r}_{p}}^{2} $$
$$ \Rightarrow {R}_{p} = {-0.0392}^{2} \approx 1.54\cdot{10}^{-3}$$
$${R}_{s} = {( \frac{{I}_{r}}{{I}_{0}}) }_{s} = {{r}_{s}}^{2}$$
$$ \Rightarrow {R}_{s} = {-0.428}^{2} \approx 0.184 $$
(4) Für den durchgehenden Strahl gilt:
$$ {T}_{p} = 1-{R}_{p}= 1-1.54\cdot{10}^{-3} \approx 0.998 $$
$$ {T}_{s} = 1-{R}_{s} = 1-0.184 \approx 0.816 $$