Du musst die beiden "Sichtstrahlen" berechnen, die durch den Betrachter und die beiden Enden des Spiegels (+10 cm und -10cm) gehen. Dann berechnest du, welcher Bruchteil des Objektes von diesen Strahlen getroffen wird, oder anders, wieviel Objekt im gelben Dreieck unten liegt. Denn da Einfallswinkel = Ausfallswinkel sowohl für das Objekt als auch für den Betrachter, werden alle Punkte innerhalb dieses Dreiecks (okay, eigentlich Kreissektors) auf einen Bildpunkt abgebildet, der innerhalb des rotbraunen Sichtfeldes liegt. Eigentlich sollte das nach links bis ins Unendliche gehen, aber ich hoffe, dass das so deutlicher ist.
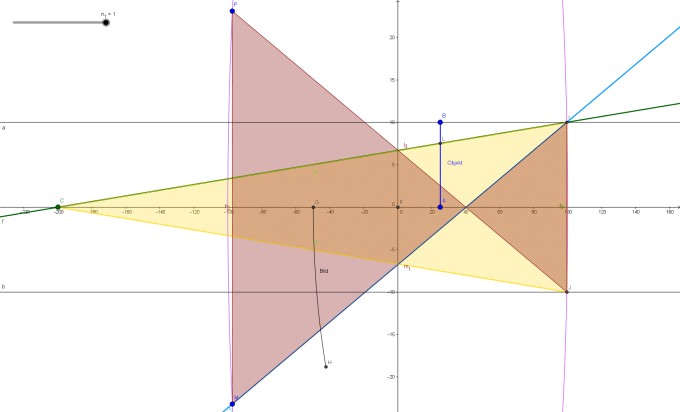
(Maßstab 5:1, damit man auch etwas erkennen kann, die horizontalen Linien sind bei +/-10cm, die violette Ellipse ist der Krümmungskreis, der Ursprung ist in der Mitte des Krümmungskeises)
Wenn du die genaue Version haben willst:
Bei einem sphärischen Spiegel gehen alle Senkrechten durch den Mittelpunkt des Krümmungskreises (der Radius steht immer senkrecht auf der Kreislinie). Also muss man zwei Spiegelgeraden ausrechnen, die jeweils ihre eigene Spiegelachse haben. Für gespiegelte Geraden gilt:
$$y(x)=d'\cdot (x-x_1)+y_1, d'=\tan\left(2\cdot\arctan\left(d_s\right)-\arctan \left(d\right)\right)$$
Dabei ist \(d\) die Steigung der gegebenen Gerade und \(d_s\) die Steigung der Spiegelachse. Der Grund: Man will denselben Winkel haben, aber auf die andere Seite der Spiegelachse gespiegelt. Also nimmt man den Winkel der Spiegelgeraden zur x-Achse \(\arctan(d_s)\) und zählt die Differenz des Spiegelwinkels und des Objektwinkels \(\arctan(d_s)-\arctan(d)\) dazu. Der Tangens macht dann aus dem Winkel wieder die Steigung.
Da in unserem Fall die Spiegelachse durch Null verläuft, ist ihre Geradengleichung: \(y(x)=\frac{y_1}{x_1}x\) für einen beliebigen Punkt \((x_1,y_1)\). Für den obersten Punkt des Spiegels wäre das \((\sqrt{10000-100},10)\). Also \(S_1:y(x)=d_sx=\frac{10}{\sqrt{9900}}x.\) S_2 hat die Steigung \(-d_s.\)
Die Geraden durch den Betrachter und den oberen/unteren Spiegelrand haben Steigung \(d_{1,2}=\pm \frac{10-0}{\sqrt{9900}+200}\).
Einsetzen in die Steigungsformel für Spiegelungen ergibt:$$d_1'=\tan(2\cdot\arctan(d_s)-\arctan (d_1))\approx 0.168527.$$ Und \(d'_2=-d_1'.\)
Also alles zwischen
\(G_1':y(x)=d_1'(x-\sqrt{9900})+10\) und
\(G_2':y(x)=-d_1'(x-\sqrt{9900})-10\)
liegt im sichtbaren Bereich.