Ein Rad kann sich frei um seine festgehaltene Achse drehen. Eine Feder verbindet eine seiner Speichen im Abstand r vom Mittelpunkt mit einer Wand.
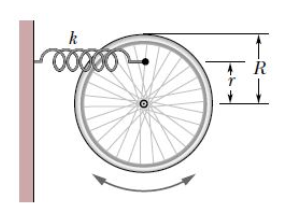
Unter der Annahme, dass sich das Rad als homogener idealisierter Ring der Masse m und des Radius R beschreiben lässt, leiten Sie einen Ausdruck für die Kreisfrequenz kleiner Schwingungen dieses Systems als Funktion von m, r, R und der Federkonstanten k her.
Hinweis: Es empfiehlt sich, dieses Problem zu lösen, indem man den Ausdruckfür die mechanische Energie des Systems in den Variablen $$x(t)\space und \space \dot{x}(t)$$ aufzuschreiben, wobei x(t) die horizontale Koordinate des Verbindungspunktes zwischen Rad und Feder ist.
Mein Ansatz hier ist, dass sich das ganze ganze ja als Pendel auffassen lässt.
Das Trägheitsmoment beträgt $$I_S = mR^2 \rightarrow I=I_S+mh^2 \rightarrow I=mR^2+mr^2=m(R^2+r^2)$$
Wenn ich nun in die Formel $$T=2\pi\sqrt\frac{I}{mgL}$$ einsetze, bekomme ich $$T=2\pi\sqrt\frac{m(R^2+r^2)}{mg(r+R)}=2\pi \sqrt\frac{R+r}{g}$$ was mich nicht weiterbringt.
Wie man das ganze nun über die Energie lösen sollte weiß ich auch nicht.
Sieht hier irgendjemand einen Weg? Wäre nett wenn ihr mir weiterhelfen könntet.
