Guten Abend,
Genau wie beim zentralen elastischen Stoß stellt man die Gleichungen zur Energie- und Impulserhaltung auf. Die Geschwindigkeit der beiden Massen \(m_1\) und \(m_2\) vor dem Stoß sei \(v_1\) und \(v_2\) und danach \(u_1\) und \(u_2\). Wir können später \(v_2\) zu 0 setzen - das ist nicht das Problem! Man erhält:
$$\frac12 m_1 {v_1}^2 + \frac12 m_2 {v_2}^2 = \frac12 m_1 {u_1}^2 + \frac12 m_2 {u_2}^2$$
$$m_1v_1 + m_2 v_2 = m_1 u_1 + m_2 u_2$$
Im Unterschied zum zentralen Stoß sind \(v\) und \(u\) aber Vektoren mit mindestens zwei Dimensionen - das heißt gerichtete Größen. In der Energiegleichung spielt dies keine Rolle, da nur die Quadrate der Geschwindigkeiten vorkommen - beim Impuls sehr wohl. In zwei Dimensionen müssen wir für \(u_1\) und \(u_2\) je zwei Koordinaten also insgesamt vier Unbekannte berechnen. Oben stehen aber nur die Energiegleichung (1 Gleichung) und die Impulsgleichung (2 Gleichungen, da Vektoren) - es fehlt also etwas. Machen wir uns zunächst ein Bild.
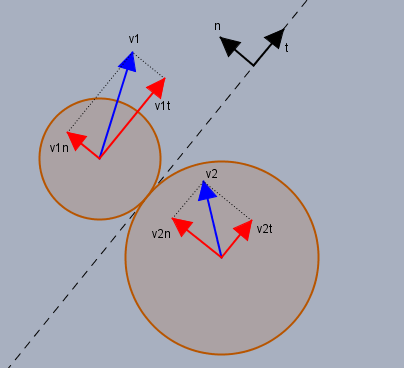
Oben siehst Du die beiden Kugeln im Augenblick der Kollision. Ich habe die Tangentialebene des Stoßpunktes eingezeichnet. Mit dem Index \(t\) in Richtung der Ebene (tangential) und dem Index \(n\) senkrecht (normal) dazu. Mit der Annahme der Reibungsfreiheit kann tangential kein Impuls zwischen den Kugeln ausgetauscht werden. Dies ist die vierte Bedingung, die wir zur Berechnung von \(u_1\) und \(u_2\) benötigen. Es muss gelten:
$$v_{1t} = u_{1t}; \quad v_{2t} = u_{2t}$$
Und für die Normalenrichtung gilt die Impulserhaltung:
$$v_{1n} m_1 + v_{2n} m_2 = u_{1n} m_1 + u_{2n} m_2$$
Wenn man nun die Energiegleichung komponentenweise aufschreibt
$$\frac12 m_1 \left( {v_{1t}}^2 + {v_{1n}}^2\right) + \frac12 m_2 \left( {v_{2t}}^2 + {v_{2n}}^2\right) \\ \space = \frac12 m_1 \left( {u_{1t}}^2 + {u_{1n}}^2\right) + \frac12 m_2 \left( {u_{2t}}^2 + {u_{2n}}^2\right)$$
und die obige Gleichheit der Komponenten in tangentialer Richtung berücksichtigt, so vereinfacht sich dies zu
$$\frac12 m_1 {v_{1n}}^2 + \frac12 m_2 {v_{2n}}^2 = \frac12 m_1 {u_{1n}}^2 + \frac12 m_2 {u_{2n}}^2$$Und damit reduziert sich das ganze Problem auf einen zentralen Stoß normal zur Stoßebene. Mit den bekannten Lösungen für die beiden Geschwindigkeitskomponenten
$$u_{1n} = \frac{ 2m_2 v_{2n} + (m_1 - m_2) v_{1n} }{m_1 + m_2}$$
$$u_{2n} = \frac{ 2m_1 v_{1n} + (m_2 - m_1) v_{2n} }{m_1 + m_2}$$
Zur Illustration rechne ich ein Beispiel mit \(v_1=v\), \(v_2=0\), \(m_2=m\), und \(m_1=4m\) sowie einer Stoßebene, die um \(30°\) gekippt zu \(v_1\) liegt. Daraus folgt: \(v_{1n}=-\cos(30°)v= - \frac12 \sqrt{3}v\) und \(v_{1t}=\sin(30°)v=\frac12 v\). die resultierenden Geschwindigkeiten sind dann (Tangential- und Normal-Richtung)
$$u_1 = \begin{pmatrix} \frac12 v\\ - \frac{3}{10} \sqrt{3} v \end{pmatrix}$$
$$u_2 = \begin{pmatrix} 0\\ -\frac{4}{5} \sqrt{3} v \end{pmatrix}$$
sieht in etwa so aus:
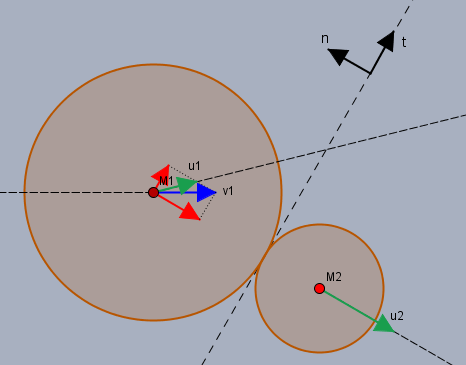
Die Geschwindigkeit von \(m_1\) vor der Kollision ist blau und die beiden Geschwindigkeiten danach sind grün eingezeichnet. Falls noch Fragen offen sind, bitte nachhaken.
Gruß Werner