Aufgabe:
Ich habe eine Frage zur a). Wieso kann R einfach durch Z ersetzt werden?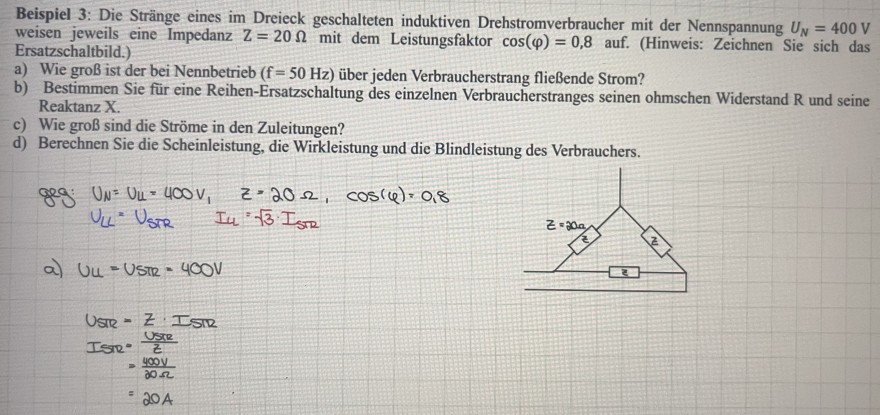
Text erkannt:
Beispiel 3: Die Stränge eines im Dreieck geschalteten induktiven Drehstromverbraucher mit der Nennspannung \( U_{N}=400 \mathrm{~V} \) weisen jeweils eine Impedanz \( Z=20 \Omega \) mit dem Leistungsfaktor \( \cos (\varphi)=0,8 \) auf. (Hinweis: Zeichnen Sie sich das Ersatzschaltbild.)
a) Wie groß ist der bei Nennbetrieb ( \( \mathrm{f}=50 \mathrm{~Hz} \) ) über jeden Verbraucherstrang fließende Strom?
b) Bestimmen Sie für eine Reihen-Ersatzschaltung des einzelnen Verbraucherstranges seinen ohmschen Widerstand R und seine Reaktanz X.
c) Wie groß sind die Ströme in den Zuleitungen?
d) Berechnen Sie die Scheinleistung, die Wirkleistung und die Blindleistung des Verbrauchers.
geg: \( U_{N}=U_{L}=400 V_{1} \quad Z=20 \Omega, \quad \cos (\varphi)=0,8 \)
\( U_{L L}=U_{S T R} \quad I_{L L}=\sqrt{3} I_{S T R} \)
a) \( U_{u}=U_{S T R}=400 \mathrm{~V} \)
\( \begin{array}{l} U_{\text {STR }} \\ = \\ \begin{aligned} I_{S T R} & =\frac{Z \text { USR }}{z} \\ & =\frac{400 \mathrm{~V}}{20 \Omega} \\ & =20 \mathrm{~A} \end{aligned} \end{array} \)