Aufgabe:
bei c) kam ich auf das richtige Ergebnis bei dem Rest allerdings nicht. Ich habe mal meine Ansätze beigefügt. 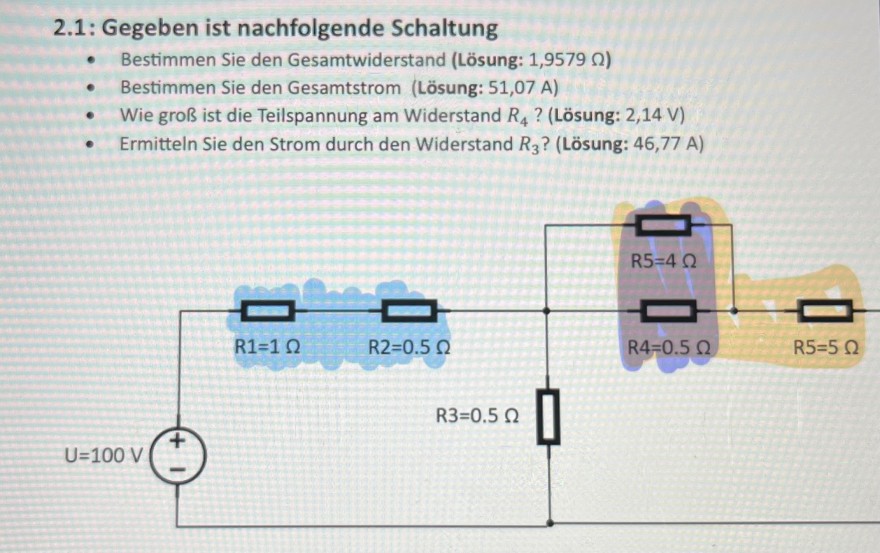
Text erkannt:
2.1: Gegeben ist nachfolgende Schaltung
- Bestimmen Sie den Gesamtwiderstand (Lösung: 1,9579 \( \Omega \) )
- Bestimmen Sie den Gesamtstrom (Lösung: 51,07 A)
- Wie groß ist die Teilspannung am Widerstand \( R_{4} \) ? (Lösung: \( 2,14 \mathrm{~V} \) )
- Ermitteln Sie den Strom durch den Widerstand \( R_{3} \) ? (Lösung: 46,77 A)

Text erkannt:
\( \begin{array}{l} \text { 2. 1) a) } R_{12}=R_{1}+R_{2} \\ \frac{1}{R_{45}}=\frac{1}{R_{4}}+\frac{1}{R_{5}} \\ R_{12}=1 \Omega+0,5 \Omega \\ \frac{1}{R_{05}}=\frac{1}{0.5 \Omega}+\frac{1}{4 \Omega} \\ R_{455} \\ \text { - } R_{45}+R_{5} \\ R_{1}=1,5 \Omega \\ \frac{1}{\mathrm{Ru}} \cdot \frac{\text { हे }}{4} \Omega \\ \text { - } \frac{4}{8} \Omega+5 \Omega \\ \text { - } \frac{49}{8} \Omega \\ R_{45}=\frac{4}{3} \Omega \end{array} \)

Text erkannt:
b)
\( \begin{array}{l} \text { Gesamistrom: Iges }=\frac{\mathrm{J}}{1008 \mathrm{~s}} \\ =\frac{1000}{1,9679 \Omega}=51,07 \mathrm{~A} \end{array} \)
c) Teilspannung bei \( \mathrm{R}_{4} \)
\( \begin{aligned} U_{4} & =R_{4} \cdot I_{4} \\ & =-95 \Omega \cdot 51,07 \mathrm{~A} \\ & =25,535 \mathrm{~V} \end{aligned} \)