Hallo
wenn da steht $$vec{r(t)}=(rcos(wt),rsin(wt),0)$$ heisst da erstmal es handelt sich um eine Kreisbewegung mit der konstanten Geschwindigkeit |v(t)|=w*t
d.h. r =const. du kannst die Bewegung aufteilen in x(t)=rcos(wt); y(t)=rsin(wt)
und damit die Geschwindigkeit in x und y Richtung einzeln betrachten x'(t)=vx(t)=-rwsin(wt) entsprechend für y'(t)=vy(t) dann x''=-rw^2cos(wt) usw.
du siehst dann dass \(\vec{a(t)}\) immer senkrecht auf \(\vec{r(t)}\) steht. Wenn r von t abhängt etwa auf einer Spiralbahn muss man natürlich auch r(t) ableiten . Wenn man eine Kurve fährt kann man sie allerdings immer in einem Punkt durch ihren Krümmungskreis ersetzen, deshalb gilt die Herleitung dann punktweise für jede Kurve, nur dass sich die Zentripetalbeschleunigung mit der Zeit ändert und man auch noch Tangentialbeschleunigungen haben kann.
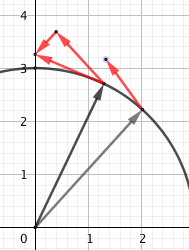
Ist es jetzt klarer? vielleicht noch mit einem Bildchen , eingezeichnet sind 2 r und rot 2 v Vektoren, von denen dann die Differenz Δv man sieht hoffentlich je kleiner der Winkel wir um so genauer geht Δv und damit Δv/Δt in Gegenrichtung zu r.