Text erkannt:
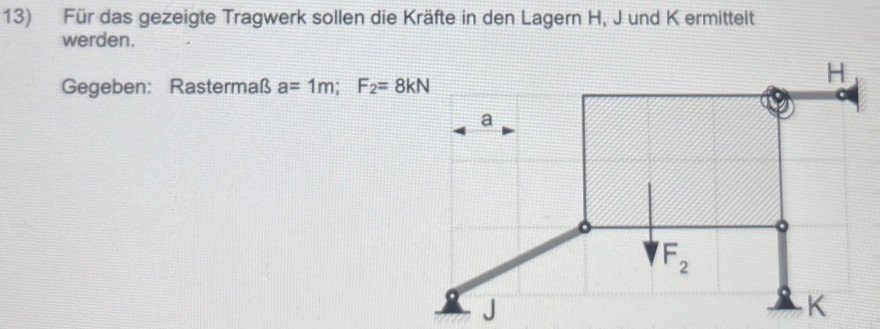
13) Für das gezeigte Tragwerk sollen die Kräfte in den Lagern \( \mathrm{H}, \mathrm{J} \) und K ermittelt werden.
Gegeben: Rastermaß \( a=1 \mathrm{~m} ; \quad F_{2}=8 \mathrm{kN} \)

Text erkannt:
13) \( \quad H=32 \mathrm{kN}(\rightarrow) ; \quad K=24 \mathrm{kN}(\uparrow) ; \quad J=35,82 \mathrm{kN} ; \quad \alpha_{J}=26,57^{\circ} \) (zur neg. \( x \)-Achse) frei:
(1) \( \Sigma F_{x} \stackrel{!}{=} 0: J_{x}+H \) \( =0 \)
(2) \( \sum F_{y} \stackrel{1}{=} 0: J_{y}-F_{z}+K \) \( =0 \)
(3) \( \sum M_{(J)} \stackrel{1}{=} 0:-F_{2} \cdot 1 m+K \cdot 3 m-H \cdot 2 m=0 \)
oder
\( \text { (4) } \sum M_{(k)} \stackrel{1}{=}=0: F_{2} \cdot 2 m-J_{y} \cdot 3 m-H \cdot 2 m=0 \)
oder
(S) \( \Sigma M_{(H)} \stackrel{!}{=} 0: F_{2} \cdot 2 \mu h+J_{x} \cdot 2 \mu h-J_{y} \cdot 3 \mu h=0 \) optimal ist (5); wg. \( \tan \alpha_{j}=\frac{1}{2}=\frac{J_{y}}{J_{x}} \) folgt:
(6)
\( J_{y}=J_{x} \cdot 0,5 \text { biw. } J_{x}=2 \cdot J_{y} \)
aus (5) folgt: \( 2 F_{2}+2 J_{x}-0,5 \cdot 3 J_{x}=0 \)
\( 2 F_{2}+0,5 J x=0 \)
darans folgt : \( J_{x}=-4 f_{2}=-32 \mathrm{kN}(\sqcup \)
Aus (1) folgt : \( H=-J_{x}=+32 k \mathrm{~N}(\rightarrow \)
Aus (2) folgt: \( K=F-J y \)
Aus(6) folgt: \( J_{y}=0,5 J_{x}=-16 \mathrm{eN}(t) \)
so forgt \( \quad K=F_{2}+16 k N=24 k N(t) \)
zusammengefaßt: \( J=\sqrt{J_{x}^{2}+J_{y}^{2}}=\sqrt{1280} \) \( J=35,777 \mathrm{kN}(\boldsymbol{A}) 206,5^{\circ} \)
zur Woogrediten: \( \alpha_{j}=\arctan \frac{J_{y}}{J_{x}}=26,565^{\circ} \)
absolut : \( \alpha_{J}=206,565^{\circ} \)
Aufgabe:
Die folgende Aufgabe ist gegeben. Ich verstehe alles bis zum rot markierten. Kann mir jemand erklären was genau dort gemacht wird ?
Woher kommt der tangens? und wie kommt kam auf Jy= Jx•0,5 bzw. Jx=2•Jy ?