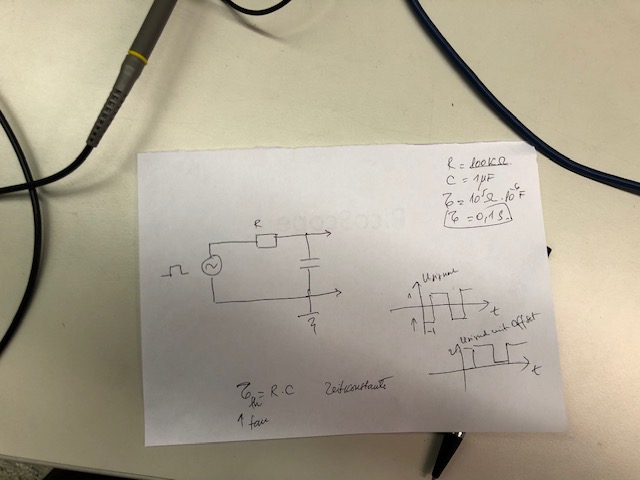
Hier wäre das Schaltbild
und zb Messwerte bei Einzelkondensatoren:
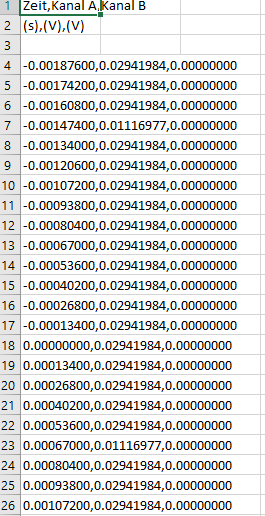
Text erkannt:
\begin{tabular}{c|l}
\hline 1 & Zeit, Kanal A,Kanal B \\
\hline 2 & \( (\mathrm{~s}),(\mathrm{V}),(\mathrm{V}) \) \\
\hline 3 & \\
\hline 4 & \( -0.00187600,0.02941984,0.00000000 \) \\
\hline 5 & \( -0.00174200,0.02941984,0.00000000 \) \\
\hline 6 & \( -0.00160800,0.02941984,0.00000000 \) \\
\hline 7 & \( -0.00147400,0.01116977,0.00000000 \) \\
\hline 8 & \( -0.00134000,0.02941984,0.00000000 \) \\
\hline 9 & \( -0.00120600,0.02941984,0.00000000 \) \\
\hline 10 & \( -0.00107200,0.02941984,0.00000000 \) \\
\hline 11 & \( -0.00093800,0.02941984,0.00000000 \) \\
\hline 12 & \( -0.00080400,0.02941984,0.00000000 \) \\
\hline 13 & \( -0.00067000,0.02941984,0.00000000 \) \\
\hline 14 & \( -0.00053600,0.02941984,0.00000000 \) \\
\hline 15 & \( -0.00040200,0.02941984,0.00000000 \) \\
\hline 16 & \( -0.00026800,0.02941984,0.00000000 \) \\
\hline 17 & \( -0.00013400,0.02941984,0.00000000 \) \\
\hline 18 & \( 0.00000000,0.02941984,0.00000000 \) \\
\hline 19 & \( 0.00013400,0.02941984,0.00000000 \) \\
\hline 20 & \( 0.00026800,0.02941984,0.00000000 \) \\
\hline 21 & \( 0.00040200,0.02941984,0.00000000 \) \\
\hline 22 & \( 0.00053600,0.02941984,0.00000000 \) \\
\hline 23 & \( 0.00067000,0.01116977,0.00000000 \) \\
\hline 24 & \( 0.00080400,0.02941984,0.00000000 \) \\
\hline 25 & \( 0.00093800,0.02941984,0.00000000 \) \\
\hline 26 & \( 0.00107200,0.02941984,0.00000000 \) \\
\hline
\end{tabular}
Wie könnte ich damit weiterarbeiten?