Hallo,
hier ein Tipp zur Lösung:
Ausgehend von dem mathematischen Zusammenhang von Spannung und Strom einer Kapazität, also
\(\large U_{C} = f(I_{C})\)
kannst Du den gesuchten Spannungsverlauf berechnen.
Die Lösung habe ich hier in das Diagramm eingetragen.
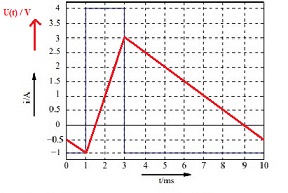
Gruß von hightech
Hallo,
hier die Berechnung des Verlaufs der Spannung:
Der Zusammenhang von Strom und Spannung einer Kapazität beschreibt die Gleichung
\(\large i_{C}(t) = C*\frac{du(t)}{dt}\)
(Diese Gleichung wird manchmal auch „das Ohmsche Gesetz einer Kapazität“ genannt.)
Diese Gleichung lässt sich nach \(\large u(t)\) umstellen
\(\large u(t) = \frac{1}{C} * \int \limits_{}^{}i(t)*dt\)
Mit dieser Gleichung lässt sich in Intervallen die gesuchte Spannung ausrechnen. Da in allen Intervallen der Strom konstant ist, wird die Berechnung des Integrals einfach.
Für die Einheit der Kapazität wird statt F die Einheit
\(\large F = \frac{As}{V}\) eingesetzt.
Intervall 0 – 1ms:
\(\large u_{1} = \frac{1}{2*10^{-3}\frac{As}{V}}*\int \limits_{0}^{1ms}(-1A)*dt\)
\(\large u_{1} = \frac{-1A}{2*10^{-3}\frac{As}{V}}*[t]_{0}^{1ms} +U_{0}\)
\(\large U_{0}\) ist die Integrationskonstane, also die Spannung zu Beginn der Integration
\(\large u_{1} = \frac{-1A}{2*10^{-3}\frac{As}{V}}*[1*10^{-3}s]_{}^{} - 0,5V\)
\(\large u_{1} = - 1V\)
Intervall 1ms -3ms:
\(\large u_{3} = \frac{1}{2*10^{-3}\frac{As}{V}}*\int \limits_{1ms}^{3ms}4A*dt\)
\(\large u_{3} = \frac{4A}{2*10^{-3}\frac{As}{V}}*[3ms-1ms]_{}^{} +U_{0}\)
\(\large u_{3} = 4V-1V = 3V\)
Intervall 3ms - 10ms:
\(\large u_{10} = \frac{1}{2*10^{-3}\frac{As}{V}}*\int \limits_{3ms}^{10ms}(-1A)*dt\)
\(\large u_{10} = \frac{-1A}{2*10^{-3}\frac{As}{V}}*[10ms-3ms]_{}^{} +U_{0}\)
\(\large u_{10} = -3,5V + 3V = - 0,5V\)
Zum Schluß noch eine allgemeine Information zum Thema Strom und Spannung einer Kapazität:
Wie oben schon gesagt ist der Strom in allen Intervallen konstant. D.h. eine Konstante integriert liefert eine linear steigende Spannung. Ein konstanter negativer Strom entsprechend eine linear fallende Spannung. Diese Eigenschaft lässt sich z.B. zur Erzeugung einer Sägezahnspannung anwenden.
Gruß von hightech