Sinus Arithmetischer Mittelwert

Question

Aufgabe:

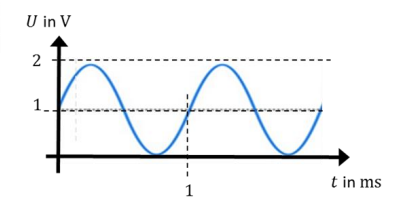
Ich möchte den Arithmetischen Mittelwert der gezeichneten Sinusfunktion berechnen.

Durch die Formel 0,637*û erhalte ich doch die Fläche unter einer Sinuswelle, korrekt? Heißt der Mittelwert ist: 2*(0,637*2)=2,54

Liege ich richtig mit meiner Annahme, oder übersehe ich etwas?

Text erkannt:

\( U \) in \( \mathrm{V} \)

(selbst erstellter Graph.)

Answer 1

Hallo Heineken0,

der arithmetische Mittelwert für diese Spannung beträgt 1V.

Hier die Berechnung:

Die Gleichung für die Wechselspannung lautet

\(\large u(t) = 1V + 1V*sin(t) = 1V*(1+sin(t))\)

Der arithmetische Mittelwert berechnet sich nach folgender Gleichung:

\(\large \overline u(t) = \frac{1}{2π}\int \limits_{0}^{2π} 1V*(1+sin(t))*dt\)

\(\large \overline u(t) = \frac{1V}{2π}*[t - cos(t)]_{0}^{2π}\)

\(\large \overline u(t) = 1V\)

Gruß von hightech

Comments

Der arithmetische Mittelwert der Wechselspannung entspricht der Fläche unterhalb der sinusförmigen Spannungskurve und berechnet sich nach folgender Gleichung

diese verbale Beschreibung entspricht nicht der folgenden richtigen Berechnung mit Bezug auf die Länge des Zeitintervalls.

------

Den Mittelwert 1 V kann man in diesem Sonderfall wohl auch einfach mit der Symmetrie des Graphen begründen. Die Nützlichkeit der Angabe der Rechnung (im Blick auf allgemeinere Fälle) bleibt davon natürlich unberührt.

---

Ich habe den Text korrigiert.