Kraft im Spreizbalken berechnen

Question

Aufgabe:

Die Kraft im Spreizbalken berechnen.

F_G = 25kN

l1= 1,7m

l2= 0,7m

l3= 0,75m

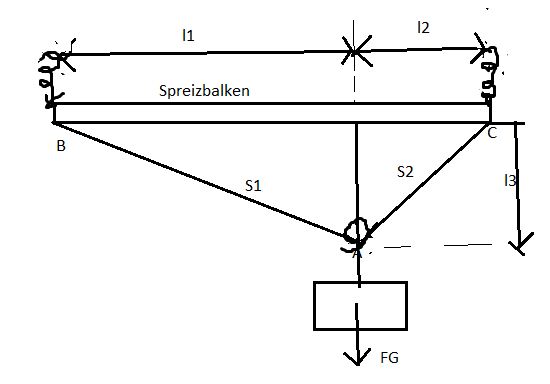
Problem/Ansatz:

Habe die Kräfte S1 und S2 jeweils in x und y Komponenten zerteilt und dann alle Kräfte jeweils(x und y Richtung) = 0 gestzt.

Habe auch durch die Länge die Winkel herausgefunden(linkes Dreieck-> unterer Winkel α= 23,8°, rechtes Dreieck unterer Winkel β= 47°).

tan(α)= G/A = 0,75m/0,7m |arctan()      <=> arctan(0,75/0,7) ≈ 47°

tan(β) = G/A = 0,75m/1,7m |arctan()    <=> arctan(0,75/1,7) ≈ 23,8°

S1x = cos(23,8°)*S1          S1y = sin(23,8°)*S1

S2x = cos(47°)*S2             S2y = cos(47°)*S2

∑Fx = 0 => 1) -S1x + S2x = 0           

∑Fy = 0 => 2) -FG + S1y + S2y =0

1) -cos(23,8°)*S1 + cos(47°)*S2 = 0                => umgeformt nach S1 = S2*cos(47°)/cos(23,8°)

2) sin(23,8°)*S1 + sin(47°)*S2 = FG

S1 in 2) einsetzen:

2) sin(23,8°)*[S2*cos(47°)/cos(23,8°)] + sin(47°)*S2 = FG

=> S2*sin(23,8°)cos(47°)/cos(23,8°) + sin(47°)*S2 = FG

=> S2*[sin(23,8°)*cos(47°)/cos(23,8°) + sin(47°)] = FG

=> S2 = FG/[sin(23,8°)*cos(47°)/cos(23,8°) + sin(47°)] = FG/[sin(23,8°)*cos(47°)/cos(23,8°) + sin(47°)]

S2= FG/[tan(23,8°)*cos(47°)/cos(23,8°) + sin(47°)] = 25.000/1,06 = 23.584,9 N ≈ 23,5 kN

S1 = 23.584,9 N * cos(47°)/cos(23,8°)  ≈ 17464,60 N ≈ 17,46 N

Komme da irgendwie nicht weiter. Vermute jedenfalls , dass man die Differenz von den beiden Kräften nehmen muss.

Glaube auch, dass ich die Kräfte S1 und S2 falsch berechnet habe.

Answer 1

Hallo user18697, ;-)

zur Aufgabenstellung: ich unterstelle, dass es sich bei \(S_1\) und \(S_2\) um reine zugbelastete Seile oder Stäbe handelt. Weiter gehe ich davon aus, dass die Last \(F_G\) nicht über eine Rolle auf ein Seil eingeleitet wird (das sieht in Deiner Skizze so aus!), sondern fixiert ist. Mit einer Rolle wäre das so nicht stabil.

Die Lagerung des Spreizbalkens selber ist nicht ersichtlich. Also geht es nur darum die Kräfte in \(S_1\) und \(S_2\) zu berechnen.

Zunächst würde ich Dir empfehlen eine massstabsgerechte Zeichnung zu machen, da kann man dann schon mal die Kräfte in etwa ablesen:

$$S_{1x}=S_{2x}\approx16,5\,\text{kN}, \quad S_{1y} \approx 7,3\,\text{kN},\quad S_{2y}\approx 17,7\,\text{kN}$$Empfehlung: Verzichte bei der Berechnung auf trigonometrische Funktionen. Hier sind die völlig unnötig. Es gilt:$$-S_{1x} + S_{2x} = 0 \\-F_G + S_{1y} + S_{2y} = 0 \\\frac{S_{1x}}{S_{1y}} = \frac{l_1}{l_3} = \frac{1,7}{0,75} \\\frac{S_{2x}}{S_{2y}} = \frac{l_2}{l_3} = \frac{0,7}{0,75}$$Löse die beiden letzten Gleichungen nach den \(S_x\)-Komponenen auf und setze diese in die erste Gleichung ein. Mulipliziere noch mit \(l_3\) und es bleibt$$\begin{aligned} -1,7S_{1y} &+&0,7S_{2y} &= 0 \\ S_{1y} &+ &S_{2y} &= 25\,\text{kN} \end{aligned}$$mit der Lösung $$S_{1y} = \frac{175}{24}\,\text{kN}, \quad S_{2y}=\frac{425}{24}\,\text{kN}, \space \implies S_{1,2x}=\frac{595}{36}\,\text{kN}$$und bleibe bis zum Schluß bei den Komponenten. Erst jetzt rechne diese mittels Pythagoras in die jeweilige Gesamtkraft um. (wenn Du sie überhaupt benötigst!)$$S_1=\sqrt{S_{1x}^2 + S_{1y}^2} \approx 18,06\,\text{kN}, \quad S_2=\sqrt{S_{2x}^2+S_{2y}^2} \approx 24,22\,\text{kN}$$

S2= FG/[tan(23,8°)*cos(47°)/cos(23,8°) + sin(47°)] = 25.000/1,06 = 23.584,9 N ≈ 23,5 kN

hier ist wie durch Zauberhand aus dem Sinus der Tangens geworden. Das ist zwar bei 23,8° ungefähr dasselbe, erklärt aber die Abweichung Deines Ergebnisses.

Gruß Werner

Comments

Vielen Dank für deine ausführliche und hilfreiche Antwort.

Laut Lösungen soll allerdings eine Kraft von 16,5 kN im Spreizbalken wirken.

Alles ist gewichtslos außer die Kraft FG.

---

Laut Lösungen soll allerdings eine Kraft von 16,5 kN im Spreizbalken wirken.

Ja - ich hätte gedacht, das steht auch so in meiner Antwort. Aber nein, nicht so direkt! Solche Sachen sind für mich so selbstverständlich, dass ich es nicht weiter erwähne.

Die Kraft \(S_{1x}\) bzw. \(S_{2x}\) muss natürlich als Druckkraft vom Spreizbalken aufgenommen werden (das sind die beiden horizontalen grünen Pfeile in der Zeichnung oben).

Die Schätzung aus der Zeichnung war \(S_x=16,5\,\text{kN}\) und die Berechnung lieferte$$S_x=\frac{595}{36}\,\text{kN} \approx 16,53\,\text{kN}$$(s.o.)

---

Und wie müsste man vorgehen, wenn man die Kraft auf dem Spreizbalken(vertikal)

-S1y-S2y-FG = 0   -S1y-S2y = FG

---

Und wie müsste man vorgehen, wenn man die Kraft auf dem Spreizbalken(vertikal) ...

ich glaub' da fehlt ein Teil Deiner Frage - oder?

Für die Kräfte innerhalb Balken muss die Lagerung desselben bekannt sein. Das ist aber aus der Aufgabenstellung nicht ersichtlich. Die Druckkraft \(S_x\) gilt streng genommen auch nur dann, wenn der Balken nicht überbestimmt gelagert ist.

Answer 2

Glaube auch, dass ich die Kräfte S1 und S2 falsch berechnet habe.

Ja, in der vorletzten Zeile hat sich ein Fehler eingeschlichen:

S2 = FG / [(sin(23,8°) * cos(47°) / cos(23,8°)) + sin(47°)]

sin(23,8°) * cos(47°) / cos(23,8°)) = tan (23,8°) * cos (47°)

und nicht : tan (23,8°) * cos (47°) / cos (23,8°)

Demnach wäre richtig:

S2 = FG / [(tan(23,8°) * cos(47°) + sin(47°)]  ≈ 24,22kN

S1 = S2 * cos(47°) / cos(23,8°) ≈ 18,05kN

Laut Lösungen soll allerdings eine Kraft von 16,5 kN im Spreizbalken wirken.

Dass sich die Ergebnisse unterscheiden, liegt daran, dass das die Seilkräfte sind, die von Werner-Salomon und mir richtig ausgerechnet wurden, aber die Aufgabenstellung etwas anderes verlangt hat.
Hilfreich wäre es gewesen, wenn du anstatt der unpräzisen Formulierung " Die Kraft im Spreizbalken berechnen." den Originalaufgabentext wiedergegeben hättest. Damit sind vermutlich die Kräfte gemeint, die aufgrund der Zugkräfte in den Seilen seitlich auf den Balken wirken und die wie folgt berechnet werden:

F_Bx = S1 * cos (23,8°) ≈ 16,5kN

F_Cx = S2 * cos (47°) ≈ 16,5kN

Comments

Danke.

Originaltext lautete : Berechnen Sie die Kraft im Spreizbalken.