wie kann man den Zusammenhang vom Ort und der Zeit von Lichtwellen verstehen? (Kohärenz)

Question

Aufgabe:

Hallöchen,

wie kann man den Zusammenhang vom Ort und er Zeit von Lichtwellen verstehen?

Problem/Ansatz:

Wir haben bereits die Unschärferelation gehabt und jetzt stehe ich auf dem Schlauch. Und zwar geht es um folgende Stelle im Skript, Kohärenz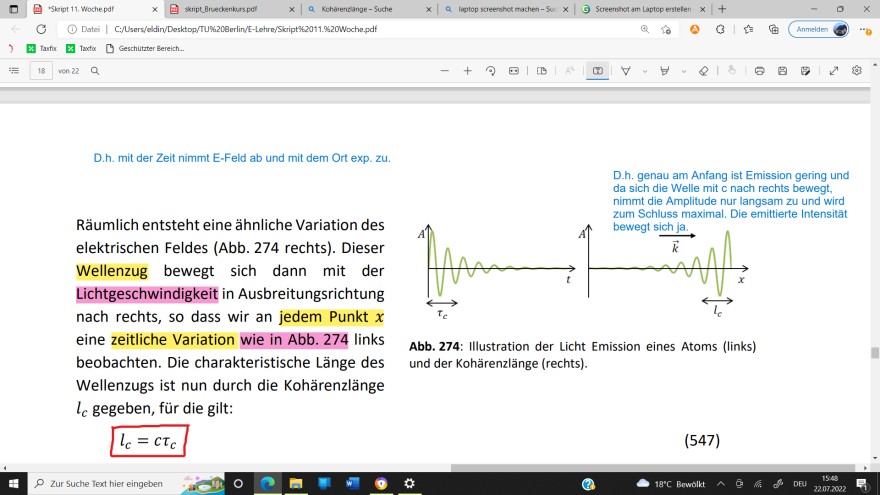

Text erkannt:

D.h. mit der Zeit nimmt E-Feld ab und mit dem Ort exp. zu. D.h. genau am Anfang ist Emission gering und da sich die Welle mit c nach rechts bewegt, nimmt die Amplitude nur langsam zu und wird zum Schluss maximal. Die emittierte Intensität Räumlich entsteht eine ähnliche Variation des elektrischen Feldes (Abb. 274 rechts). Dieser Wellenzug bewegt sich dann mit der Lichtgeschwindigkeit in Ausbreitungsrichtung nach rechts, so dass wir an jedem Punkt \( x \) eine zeitliche Variation wie in Abb. 274 links
Abb. 274: Illustration der Licht Emission eines Atoms (links)
beobachten. Die charakteristische Länge des und der Kohärenzlänge (rechts).
Wellenzugs ist nun durch die Kohärenzlänge
\( l_{c} \) gegeben, für die gilt:
\( l_{c}=c \tau_{c} \)

Answer 1

Hallo

die Unschärferelation von Energie und Zeit, bestimmt das Zeitintervall Δt=τc in dem die Lichtwelle ausgesandt wird. die Länge des Wellenzuges l=c*τc ist deshalb endlich, Wenn sich nun bei einem Experiment 3 solche Wellen treffen können sie nur interferieren (also sich gegenseitig verstärken oder abschwächen) , wenn der Wegunterschied von der Quelle zum Treffpunkt kleiner ist als diese Länge. deshalb heisst sie Kohärenzlänge, nur dan haben die 2 Wellenzüge noch etwa miteinander zu tun sind also "kohärent!

Gruß lul

Comments

Warum muss die Kohärenzlänge größer sein als die weglänge?

---

Langer als der Wegunterschied, nicht die Weglänge, sonst treffen sich die 2 Wellenstücke ja gar nicht.