Komplexes Widerstandsnetzwerk berechnen

Question

Text erkannt:

\( B \)

Aufgabe:

…

Man bestimme den Widerstand zwischen den Klemmen A und C, wobei alle Widerstände die Größe R haben.

Problem/Ansatz:

In der Aufgabe davor sollte man den Widerstand zwischen A und B bestimmen, was ich auch geschafft habe, weil ja wegen der Symmetrie im horizontalen Zweig kein Strom fließt. Aber mir fehlen die Ideen für den Ersatzwiderstand zwischen A und C. Ich habe schon die Potenziale angeschaut und auch die Ströme, weil ich eventuell mit Kirchhoff ansetzen wollte. Aber da sind so viele Knoten, sodass es viel zu viele Ströme sind.

Kann mir jemand vielleicht einen Tipp geben?

Ich wäre für jede Hilfe sehr dankbar! ;)

Answer 1

Hallo,

hier die Lösung:

Die beiden Quadrate Rot und Blau in Bild 1 stellen je eine Dreieckschaltung dar, die in eine Sterschaltung umgerechnet werden können.

Bild 1:

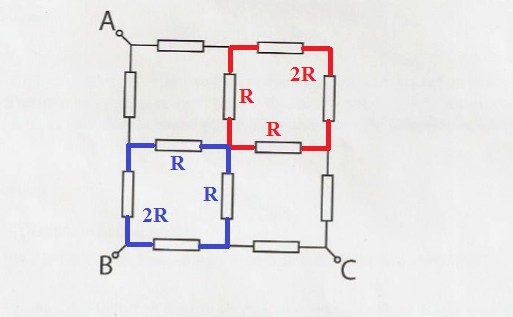
Bild 2 zeigt die umgerechneten Werte:

Bild 2:

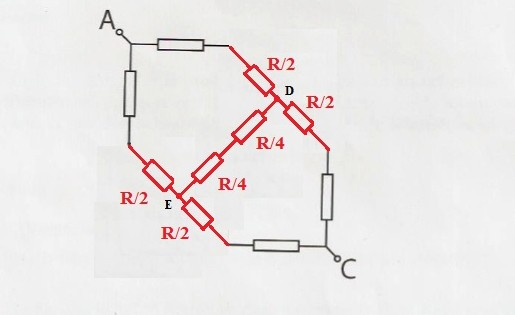
Da die Punkte D und E aus Symmetriegründen auf gleichem Potential liegen, kann D mit E verbunden werden, Bild 3.

Bild 3:

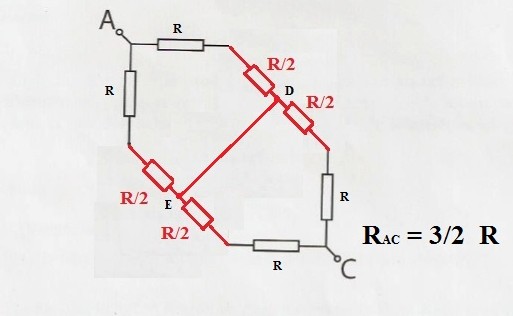
Der Widerstand zwische A und C kann jetzt berechnet werden:$$R_{A,C} = \frac{3}{2} * R$$

Aber auch ohne die Verbindung zwischen D und E lässt sich beweisen, dass  \(R_{A,C} = \frac{3}{2} * R\)

Ausgehend von Bild 2 werden hierzu die grün markierten Widerstände der Dreieckschaltung in Bild 4 in eine Sterschaltung umgerechnet.

Bild 4:

Die umgerechneten Werte zeigt Bild 5.

Auch hier ergibt sich ein Gesamtwiderstand   \(R_{A,C} = \frac{3}{2} * R\)

Gruß von hightech