Flugbahn von zwei geladenen Teilchen berechnen

Question

Aufgabe: Flugbahn von zwei geladenen Teilchen berechnen

Problem/Ansatz: Ich moechte die Flugbahn von zwei geladenen Teilchen berechnen.

Exakt: Fuer einen bestimmten Zeitpunkt t moechte ich die exakten 3 dimensionalen Koordinaten

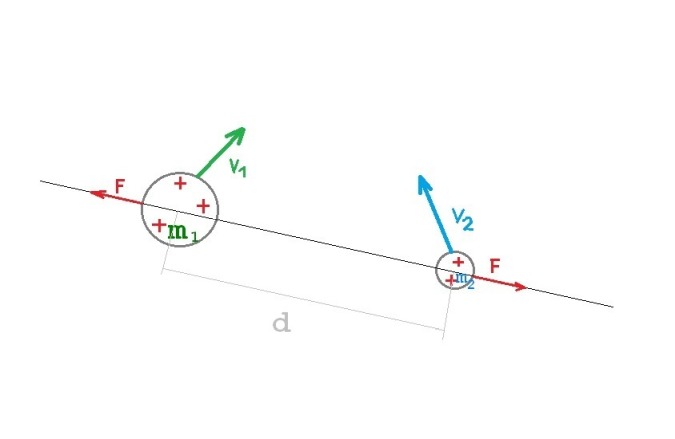
berechnen. Zwei geladene Teilchen (siehe Skizze unten) mit der Masse m₁ und m₂

und der Ladung Q₁ und Q₂ bewegen sich zum Zeitpunkt t₀ mit den Geschwindigkeiten v₁ und v₂.

Zu diesem Zeitpunkt t₀ befinden sie sich an den Orten P₁(x,y,z)  und P₂(x,y,z).

Auch die Geschwindigkeiten sind Vektoren.

Auf die Teilchen wirkt die Kraft  F (Coulombkraft) . ( Die Teilchen stossen sich ab; sind beide

positiv geladen)

                             F= k * (Q_1*Q₂) / d²

wobei d der momentane Abstand zwischen den Teilchen ist. Durch die Kraft F veraendern

sich die Geschwindigkeitsvektoren v₁ und v₂ staendig. Durch das 2. Newton´sche Gesetz

( F= m*a) wissen wir, dass ein Koerper mit der Masse m, auf den die Kraft F einwirkt,

eine Beschleunigung a erfaehrt. So haben wir fuer Teilchen 1 : a₁= F/m₁  bzw a₂= F/m₂

Setzen wir fuer F obige Formel ein, erhalten wir a₁=k*(Q₁*Q₂) / (m_{1 *} d²).

Dieses a₁ bzw a₂  veraendert jetzt v₁ bzw v₂.

Wie kann ich jetzt fuer einen bestimmen Zeitpunkt den Ort der Teilchen berechnen ?

Ich habe mir folgendes ueberlegt: Zum Anfangszeitpunkt t₀ kenne ich die genauen Koordinaten

der Teilchen, ich kenne v₁ und v₂ und auch a₁ und a₂. Fuer ein sehr kurzes Zeitintervall Δt koennte

ich nun die veraenderte Geschwindigkeit v_1a berechnen :

     v_1a = v₁*a₁*Δt

Aber mein Problem ist, waehrend Δt ist a₁ nicht konstant, sondern aendert sich auch,

weil sich die Teilchen ja bewegen. Der Fehler ist zwar umso kleiner je kleiner ich Δt waehle,

aber exakt ist das nicht.

Koennte diese Aufgabe mit einer Differentialgleichung geloest werden ?

Die Ableitung von v₁ sollte a₁ sein.   v₁´ = a₁

Aber v₁ ist ja ein Vektor. Irgendwie steh ich an. Kann mir da bitte jemand weiterhelfen  ??  :))

liebe Gruesse

Andreas / Wien

Text erkannt:

\( \frac{F}{+\frac{+m_{j}}{d}+} \underbrace{v_{1}}_{d_{i}+i_{2}} \)

Answer 1

Hallo,

ja, das läuft auf das lösen einer Differentialgleichung hinaus.

Das ist ein klassisches Zweikörperproblem. Das löst man durch Übergang zu Schwerpunkt- und Relativkoordinaten.

Das hier alles aufzuschreiben ist relativ umständlich.

Da die Coulombkraft dieselbe Abhängig vom Abstand aufweist wie die Gravitationskraft, läuft es auf das Keplerproblem heraus.

Schau mal hier:

https://de.wikipedia.org/wiki/Zweik%C3%B6rperproblem

oder hier ganz ausführlich ;)

https://www.lsw.uni-heidelberg.de/users/mcamenzi/HD_Kepler.pdf