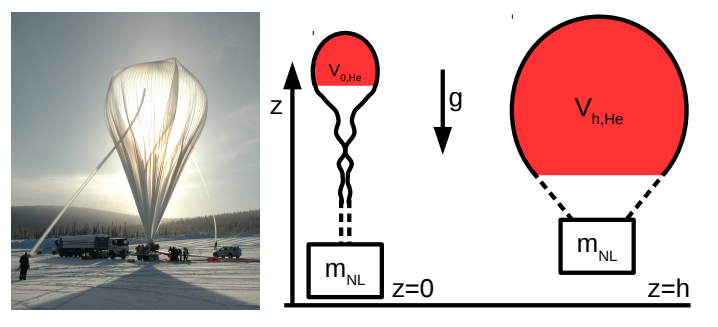
Mit der studentischen Forschungsballonmission BEXUS werden Nutzlasten von etwa \( m_{\mathrm{NL}}=70 \mathrm{kg} \) in Form
von Messgeräten und Versuchsaufbauten in eine Missionshöhe von \( h=25 \mathrm{km} \) befordert, wo dann Versuchs-
zeiten in der Stratosphäre von bis zu fünf Stunden möglich sind. Die Masse des verwendeten Ballons (Hülle,
Struktur, Elektronik, Landeschirm) beträgt etwa \( m_{\mathrm{B}}=170 \mathrm{kg} . \) Die unten ständig offene Hulle des verwende-
ten Gleichdruckballons wird am Startplatz mit Helium betankt, so dass diese zunächst schlaff gefallt ist und
sich während des Aufstieges ungehindert entfalten kann. Bitte lesen Sie die Aufgabe zunächst ganz durch und
beachten Sie die gegebenen Größen und Hinweise am Ende des Aufgabenblattes.
a) Für den Missionstag ist am Startplatz auf Meeresniveau \( (z=0 \mathrm{m}) \) kühles, trockenes Wetter bei \( p_{0}=1 \) bar, \( \rho_{0}=1 \mathrm{kg} \mathrm{m}^{-3} \) und \( t_{0}=6.85^{\circ} \mathrm{C} \) vorhergesagt. Berechnen Sie die Skalenhöhe \( H \) für die aktuellen Witterungsbedingungen, welche in die relevanten Atmosphärenmodelle eingeht.
b) Wie groß sind der Druck \( p_{h} \) und die Temperatur \( T_{h} \) in der Missionshohe \( h \) unter der Annahme einer
isentropen Schichtung der Atmosphäre? Runden Sie die berechneten Werte auf die erste signifikante
Stelle und tragen diese in die vorhandenen Diagramme in Abb. 2 ein. Bewerten Sie das isentrope
und das isotherme Modell für das Einsatzgebiet Stratosphäre an Hand der internationalen Standard
Atmosphäre (ISA) in wenigen, qualitativen Stichworten.
c) Welche Menge Helium \( \left(m_{H e} \text { in } \mathrm{kg}\right) \) muss der Tankwagen am Startplatz mindestens mit sich führen, \right.
damit der Ballon unter Vernachlầssigung aller Verluste und Störungen mit der Nutzlast \( m_{\mathrm{NL}} \) überhaupt
vom Boden abheben kann?
d) Welche Fläche an Ballonseide \( \left(A_{B} \text { in } \mathrm{m}^{2}\right) \) wird zur Fertigung der Hülle mindestens benötigt (ohne Nahtzugaben etc.), damit der Ballon inklusive Nutzlast \( m_{\mathrm{NL}} \) die Missionshöhe \( h \) erreichen kann? Gehen Sie dabei von einer isothermen Atmosphärenschichtung aus und lesen sie die dafür nötigen Größen
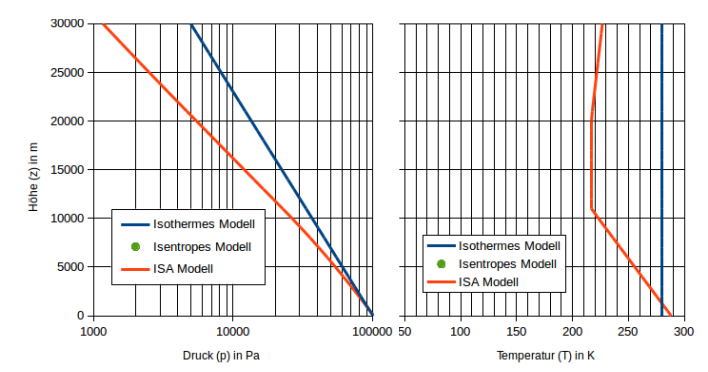
Abbildung 2: Atmosphärenmodelle: isotherm, isentrop, und internationale Standardatmosphäre (ISA). Errechnete Werte aus Aufgabenteil b) sollen auf die erste gultige Stelle gerundet und in dieses Diagramme eingetragen werden. Zeichnen Sie also 2 einzelne Datenpunkte ein und nehmen Sie dann einen qualitativen Vergleich in knappen Stichworten vor:
gegebenenfalls aus dem vorhandenen Diagramm in Abb. ?? ab (auf die erste signifikante Stelle genau).
Vereinfachend soll die voll entfaltete Ballhülle als ganze Kugel angenommen werden.
Gegeben:
Kreiszahl \( \pi \approx 3.0 \) - Erdbeschleunigung \( g \approx 10 \mathrm{m} \mathrm{s}^{-2} \) - Isentropenexponent trockner Luft \( \kappa_{\mathrm{Luft}}=1.4=7 / 5 \) - Dichte von Helium am Startplatz \( \rho_{0, \mathrm{He}} \approx 0.2 \mathrm{kg} \mathrm{m}^{-3} \) - Volumen einer Kugel \( V_{K}=\frac{4}{3} \pi r^{3} \) - Oberfläche einer Kugel \( A_{K}=4 \pi r^{2} \) - Numerische Werte einiger nützlicher Potenzen - Lơsungshinweise Die Skalenhöhe H wird durch den Druck, die Dichte und die Gravitationsbeschleunigung charakterisiert. Druckverlauf bei isentroper Atmosphärenschichtung: \[ p_{h}=p_{0}\left(1-\frac{\kappa-1}{\kappa} \frac{z}{H}\right)^{\frac{s}{\kappa-1}} \]

ich habe alles berechnet bis Aufgabenteil b)
ph habe ich berechnet und muss noch Th berechnen und das ganze in Diagramm eintragen!
Welche formel brauche ich für Th
Th =T0 *(ph/p0 = (6,85°C+273-(1247Pa/1000Pa)(1,4-1)/1,4 =298,068 K
ist das richtig hier was ich berechnet habe?
Gruß