Potentielle Energie einer Doppelfeder.

Question

Die Bewegungsgleichung eines ebenen mechanischen Systems soll mit Hilfe der Lagrange’schen Gleichungen zweiter Art ermittelt werden. Das System besteht aus den Massen m_1 und m_2, welche reibungsfrei gelagert sind. Die Federn (Federsteifigkeiten k bzw. c) sind entspannt für die Lage der Massenschwerpunkte im Ursprung des Inertialsystems mit den Achsen x und y. Die verallgemeinerte Koordinate q_1 beschreibt die Verschiebung der Masse m_1 bezüglich des Inertialsystems, die verallgemeinerte Koordinate q_2 beschreibt die Verschiebung der Masse m_2 bezüglich der Masse m_1. Der Winkel α ist konstant.

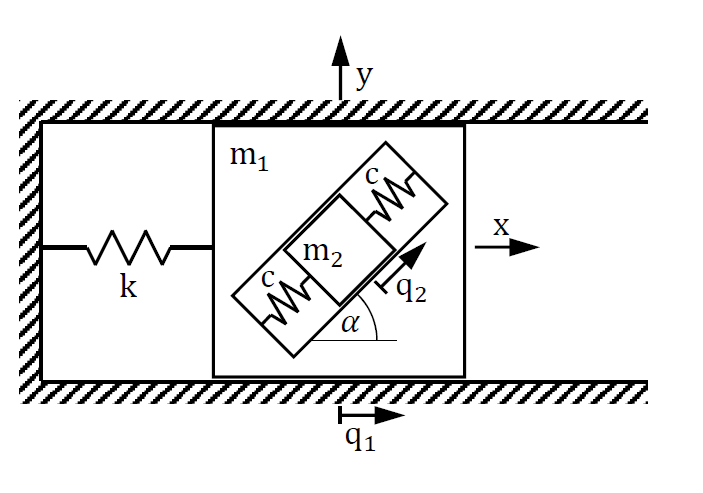
Es geht um die Potentielle Energie der Federn c bei m_2. Mir gehts nur um die Feder hier. Da die Energie von m_2 leicht ist.

in der Musterlösung steht: V = c·q₂ ² 

Ich weiß nicht, ob ichs richtig verstanden habe. Hier ist mein Weg:

\( \frac{1}{2}\left(q_{2}-0\right)^{2}-\left(-\frac{1}{2}\left(q_{2}-0\right)^{2}\right)=c q_{2}^{2} \)

Wir ziehen von der unteren Feder die Obere ab, da die obere ja wieder runterdrückt.

Aber die obere ist negativ, da in q_2 richtung, die Feder eingedrückt wird und somit die Kraft runter wirk. also negativ.

ist das richtig?

mfg

Answer 1

Hallo

 nein, du kannst nicht 2 Energien voneinander abziehen, die eine Feder wird gedehnt um q₂, die andere um q₂ zusammengedrückt, also hat man einfach 2*c/2*q₂^2addieren könntest du die Kräfte, wenn du nach rechts verschiebst wird eine Feder zusammengedrückt, Kraft also nach links, die andere gedehnt also auch Kraft nach links, so dass du insgesamt die Kraft F=-2q*c hast integriert dann die Energie c*q^2

Gruß lul

Comments

ok verstehe.

und nach rechts schieben wäre in diesem fall die kraft der feder k?

die wäre -qc -> integr. -> -1/2cq²? bei deinem beispiel hast du die - vergessen glaub ich. oder wird bei energie immer der Betrag genommen? bzw. woher weiß ich ob + oder -?

und zu pot. energie von m_2... ich habe gedacht = 0, da die beiden federn das ausgleichen? eine drückt hoch, die andere runter. und m_2 hat somit keine energie, da die höhe 0 ist?