Hi,
die Geschwindigkeit des Verfolgungsfahrzeuges ist proportional zum Abstand der beiden Fahrzeuge, d.h. \( v_2 = \alpha \cdot \Delta \) mit \( \alpha = \) Proportionalitätskonstante und \( \Delta = s_1 - s_2 \) wobei \( s_{1,2} = \) die Positionen der beiden Fahrzeuge zum Zeitpunkt \( t \) sind.
Da zum Abstand \( L \) der beiden Fahrzeuge, das Verfolgungsfahrzeug die Geschwindigkeit \( v \) hat, folgt \( \alpha = \frac{v}{L} \)
Weiter gilt \( s_2 = \alpha \cdot \Delta = \frac{v}{L} ( 2 \cdot v \cdot t - s_2 ) \cdot t \). Daraus ergibt sich
$$ s_2 = \frac{2 \cdot v^2 \cdot t^2}{L+v \cdot t} $$ Die Geschwindigkeit des Verfolgungsfahrzeuges ergibt sich durch differenzieren des Weges nach der Zeit zu $$ v_2 = 2 \cdot t \cdot v^2 \cdot \frac{2L+tv}{(L+tv)^2} $$
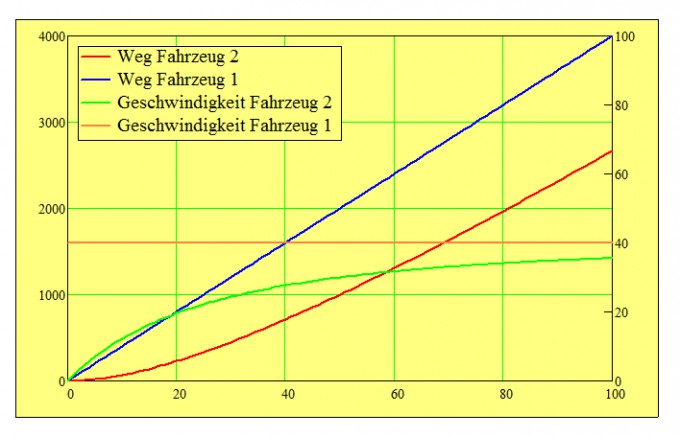
Für \( v = 20 \) und \( L = 1000 \) sieht das folgendermaßen aus.
Die Wege sind auf der linken Skale abgetragen, die Geschwindigkeiten auf der rechten.