Hallo Solaris,
am Sonntag kam was ungeplantes dazwischen, daher wird die Antwort hier etwas kürzer.
Zunächst mal gilt es, ein geeignetes Koordinatensystem zu wählen und die Lage der Module darin zu beschreiben. Danach projiziert man eine Modulreihe in Sonnenrichtung auf die dahinter liegende und bestimmt dann den Schnitt des Vorgängerschattens mit dem Nachfolger. Letzteres ist in meinen Augen der schwierigere Part.
Da hast nun nicht beschrieben, wie Ihr die Lage der Module beschreiben wollt, daher hier mein Vorschlag. Als X-Achse definiere ich die unterste Querlattung der ersten Modulreihe (der Sonne am nächsten stehend). Die Z-Achse zeige senkrecht nach oben und die Y-Achse steht dann auf beiden senkrecht und rechtsdrehend, d.h. sie horizontal zeigt nach hinten zu den Nachfolgemodulen.
Das lokale Koordinatensystem eines Streifens ist am linken Rand um \(d=0,4) von der unteren linken Ecke nach oben versetzt. Die X-Richtung läuft quer zum Streifen und die Y-Richtung in Längsrichtung. Ich habe dies mal im Geoknecht3D eingegeben und exemplarisch drei vertikale Streifen skizziert. Zunächst aber ein Streifen in '0'-Position:
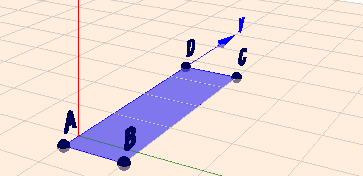
(klick auf das Bild und rotiere die Szene mit der Maus)
Die vier Ecken \(ABCD\) liegen dann bei den lokalen Koordinaten: $$^SA= \begin{pmatrix} 0\\ -d\\ 0 \end{pmatrix} \quad {^SB}= \begin{pmatrix} b\\ -d\\ 0 \end{pmatrix} \quad {^SC}= \begin{pmatrix} b\\ l-d\\ 0 \end{pmatrix} \quad {^SD}= \begin{pmatrix} 0\\ l-d\\ 0 \end{pmatrix}$$ ich habe die Koordinaten mit einem hochgestellten \(S\) für 'Streifen' versehen, da dies die Koordinaten im 'Streifensystem' sind.
Mit folgenden Daten (dimensionslos): Streifenbreite \(b=1\), Streifenlänge \(l=4\), Neigungswinkel gegenüber der Horizontalen \(\varphi=20°\) und Drehwinkel um die lokale horizontale Achse \(\gamma=35°\) - sieht es dann so aus:
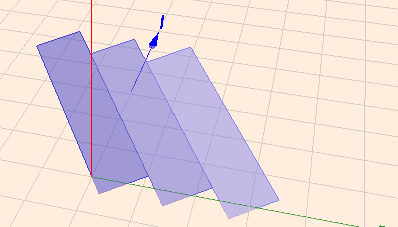
Man kommt zu den Positionen im Raum, indem man die lokale Lage (s.o.) in zwei Schritten in die globale transformiert. Eine Drehung um die X-Achse um \(\varphi\) (in homogenen Koordinaten):
$$^0T_1= \begin{pmatrix} 1 & 0 & 0 & \frac{i \cdot b}{\cos \gamma}\\ 0 & \cos \varphi & -\sin \varphi& 0 \\ 0 & \sin \varphi& \cos \varphi& 0\\ 0 & 0 & 0 & 1\end{pmatrix}$$ Der Index \(i\) ist der Index des Streifens. Der linke Streifen hat den Index \(0\) der zweite \(1\), dann \(2, \, 3, 4, \) usw. Anschließend werden die Streifen um ihre lokale Z-Achse um \(\gamma\) in die Position \(S\) gedreht (\(S\) für Streifen):
$$^1T_S= \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 & 0 \\ \sin \gamma & \cos \gamma & 0& 0 \\ 0 & 0& 1& 0\\ 0 & 0 & 0 & 1\end{pmatrix}$$ Die Gesamttransformation ist dann die Multiplikation der beiden Matrizen
$$^0T_1 \cdot {^1T_S} = {^0T_S} = \begin{pmatrix} \cos \gamma & -\sin \gamma & 0 &\frac{i \cdot b}{\cos \gamma} \\ \sin \gamma \cdot \cos \varphi & \cos \gamma \cdot \cos \varphi& -\sin \varphi & 0 \\ \sin \gamma \cdot \sin \varphi & \cos \gamma \cdot \sin \varphi& \cos \varphi& 0\\ 0 & 0 & 0 & 1\end{pmatrix}$$ nun kann man die Position der Ecken damit berechnen. So ist z.B.: $$^0A = {^0T_S} \cdot {^SA}$$
Mag sein, dass das für Dich etwas kompliziert aussieht. Die Arbeit mit den Matrizen hat aber den Vorteil, das man sie bequem in ein Tabellenkalkulationsprogramm eingeben und ausrechnen kann. Insbesondere wenn man nicht nur eine Transformation sondern - wie hier - einen ganzen Haufen hat. Was anderes habe ich hier auch nicht gemacht, als ich die Daten im Geoknecht3D eingegeben habe.
Fortsetzung 2.Teil:
Im ersten Teil habe ich gezeigt wie man alle Punkte einer Modulreihe im 3-dimensionalen berechnet. Nun projiziere ich einen Punkt auf die nachfolgende Modulreihe. Dazu benötige ich die Richtung, in der die Sonne steht. Als Azimut \(\alpha\) wähle ich den Winkel zur \(X-Achse\) rechtsdrehend zur Y-Achse. D.h. wenn die Sonne im Süden der Module steht, so wäre \(\alpha=-90°\) und bei \(\alpha=0°\) steht sie im Osten der Module (Bem.: das ist keine Beschreibung, wie sie in der Astronomie üblich ist!) Die Altitude \(h\) sei der Winkel über der XY-Ebene. Bei \(h=0°\) steht die Sonne auf dem Horizont und bei \(h=90°\) im Zenit. Zusammen mit einem beliebigen Punkt \(P_1\) - z.B. einer oberen Ecke eines Modulstreifens - kann ich nun die Geradengleichung des Schattenstrahls \(s\) von dieser Ecke aus aufstellen. Es ist $$s_1: \space x = P_1 + \begin{pmatrix} \cos\alpha \cdot \cos h\\ \sin \alpha \cdot \cos h \\ \sin h \end{pmatrix} \cdot t$$
um dies mit der nächsten Modulreihe zum Schnitt bringen muss ich zunächst die zweite Reihe beschreiben. Dazu definiere ich eine Lage der zweiten Reihe gegenüber der ersten. Ist die zweite Reihe nur um die Distanz \(e\) in Y-Richtung verschoben, so wäre die Position \(Q_2\): $$^0Q_2 = \begin{pmatrix} 0 \\ e \\ 0 \end{pmatrix}$$ und die Transformationsmatrix \(^0T_{Q2}\) ist $$^0T_{Q2} = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & e \\ 0 & 0 & 1 & 0\\ 0& 0&0 & 1\end{pmatrix}$$ und die Transformation \(^0T_{S2}\) zu den einzelnen Streifen ist nun $$^0T_{S2} = {^0T_{Q2}} \cdot ^0T_S$$ Dieser Matrix kann ich nun einen Punkt \(p_2\) (die vierte Spalte) und einen Normalenvektor \(n\) (die dritte Spalte) entnehmen und sofort die Hessesche Normalform der Ebene \(E_2\) der zweiten Modulreihe aufstellen: $$E_2: \space n \cdot x = n \cdot p_2$$ (Bem.: bemerkst Du die Vorteile dieser Matrizen?) Diese Ebene und den Schattenstrahl kann ich nun zum Schnitt bringen (das erkläre ich hier nicht!) und erhalte den Schnittpunkt \(^0P_1'\) im 0-System.
Um festzustellen, wo \(P_1'\) auf der Modulreihe liegt transformiere ich ihn in das \(S2\)-System. Es ist $$^{S2}T_0 = \left({^0T_{S2}}\right)^{-1}$$ also die Inverse der bereits bekannten Matrix und die gesuchte Position \(^{S2}P_1'\) ist: $$^{S2}P_1' = {^{S2}T_0} \cdot {^0P_1'}$$ Die Z-Koordinate sollte =0 sein, wenn man sich nicht verrechnet hat(!) und X- und Y beschreiben die lokale Position -so wie hier:
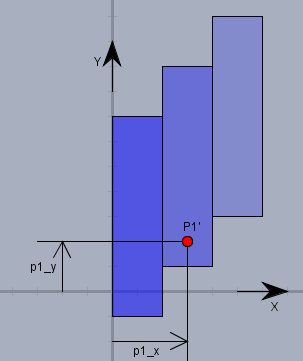
Aus der X-Koordinate lässt sich der Streifen und die X-Position auf dem Streifen bestimmen und aus der Y-Koordinate lässt sich ablesen, ob der Schattenpunkt überhaupt auf einem Streifen liegt oder nicht.
... es soll noch einen dritte Teil geben
Es wäre hilfreich, wenn Du mir inzwischen Feedback gibst ob Du mit meiner Antwort was anfangen kannst und was Du evt. nicht verstehst.
Gruß Werner