Hallo Applwind,
Fährt das Schiff nach Süden so bläst auch der Fahrtwind \(f=16\text{m/s}\) aus südlicher Richtung und der scheinbare Wind \(s\), das heißt, der Wind den ein Passagier an Bord spürt, ist die Summe aus Fahrtwind und wahrem Wind \(w=8\text{m/s}\) aus NO. Eine Sizze zeigt die Verhältnisse:
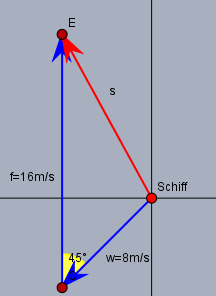
Und der Betrag des scheinbaren Windes \(s\) lässt sich mit Hilfe des Cosinussatzes berechnen:
$$s^2 = w^2 + f^2 - 2wf \cdot \cos(45°) = \left( 8 \frac{\text{m}}{\text{s}} \right)^2 + \left( 16 \frac{\text{m}}{\text{s}} \right)^2 - 2 \cdot 8 \frac{\text{m}}{\text{s}} \cdot 16 \frac{\text{m}}{\text{s}} \cdot \frac12 \sqrt{2}$$
$$\Rightarrow \space s \approx 11,8 \frac{\text{m}}{\text{s}}$$