Vom Duplikat:
Titel: Stehaufmännchen. Wie berechne ich die Lage des Schwerpunktes und die maximale Höhe h?
Stichworte: kegel,radius,schwerpunkt,physik,prüfung,kraft,mathearbeit
Hallo,
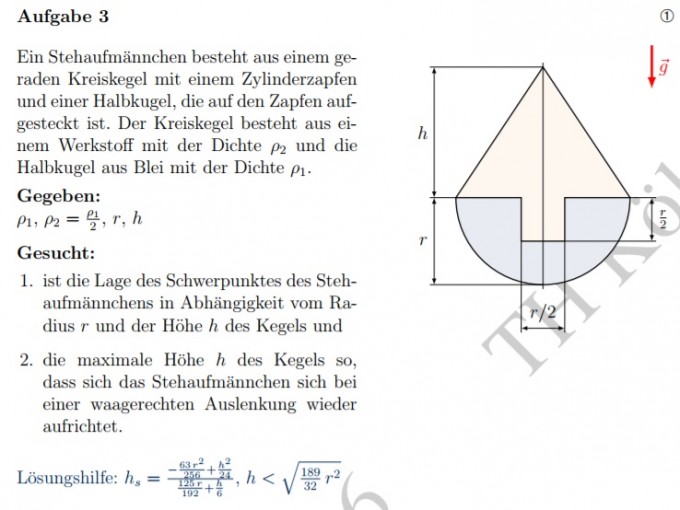
Die Aufgabe: (siehe Anhang für Aufgabe+Darstellung) Ein Stehaufmännchen besteht aus einem geraden Kreiskegel mit einem Zylinderzapfen und einer Halbkugel, die auf den Zapfen aufgesteckt ist. Der Kreiskegel besteht aus einem Werkstoff mit der Dichte p2 und die Halbkugel aus Blei mit der Dichte p1.
Gegeben: p1 ,p2 = p1/2 ,r , h
Gesucht:
1. ist die Lage des Schwerpunktes des Stehaufmännchens in Abhängigkeit vom Radius r und der Höhe h des Kegels und
2. die maximale Höhe h des Kegels so, dass sich das Stehaufmännchen sich bei einer waagerechten Auslenkung wieder
aufrichtet.
Meine Frage: Ich komme gar nicht klar wie ich die beiden Aufgaben lösen kann, würde mich echt auf Erklärungen freuen :) . Die beste Antwort wird markiert (PS: Ich bereite mich auf eine Prüfung vor)
Anhang:
Aufgabe