Hallo Namur,
Du fragst nach der Formel? Ich meine, Du hast mehr Erfolg Aufgaben dieser Art zu meistern, wenn Du Dich mehr mit den Zusammenhänge beschäftigst, die dabei eine Rolle spielen. Ein Schiff fährt mit konstanter Geschwindigkeit, eine Kraft (Wind) wirkt auf es ein. Der Winkel von Kraft zu Fahrtrichtung sind \(60°\) - mache Dir eine Skizze:
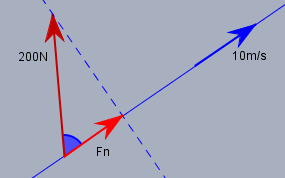
Es sollte intuitiv verständlich sein, dass nur der Teil der Kraft eine Wirkung auf die Fahrleistung des Schiffes hat, welcher in Richtung der Fahrt wirkt. Dazu projiziert man die Kraft auf die Fahrtrichtung. Weniger mathematisch gesprochen lässt man die Spitze des Kraftvektor senkrecht auf die Fahrrinne plumsen. Wenn ich Dir jetzt sage, dass \(F_n=F\cdot \cos{(60°)}\) ist, kannst Du das auch gleich wieder vergessen. Bei Winkeln von \(60°\) oder \(30°\) sind immer irgendwelche gleichseitigen Dreiecke im Hintergrund, so wie hier auch
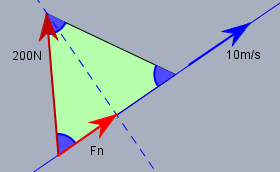
Und siehe da (siehst Du es auch?) \(F_n\) muss genau halb so groß sein, wie die Kraft selbst. Und wenn nun nach der Leistung gefragt ist (und nicht nach der Kraft), so ist die Leistung \(P\) gleich Kraft \(F\) mal Geschwindigkeit \(v\). So wie beim Auto: umso mehr Beschleunigung (Kraft) und umso mehr Geschwindigkeit, desto mehr Leistung - also
$$P = F_n \cdot v = \frac{1}{2} \cdot 200 \text{N} \cdot 10 \frac{\text{m}}{\text{s}}= 1000 \text{W}$$
Gruß Werner