Hallo,
Dadurch dass der Winkel von \(129°\) bereits vorgegeben ist, gibt es keine Kraft \(F_3\) unter \(129°\) zu \(F_1\), die das Kräftegleichgewicht erfüllt. Folgende maßstabsgetreue Skizze zeigt den Zusammenhang.
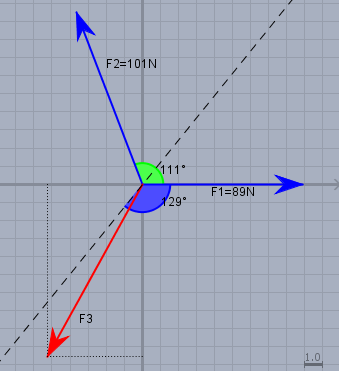
Ich habe \(F_1\) so gelegt, dass die Kraft in positive X-Richtung zeigt - daher ist die Skizze gegenüber Deiner nach links gedreht. Die gestrichelte Linie zeigt die Richtung von \(129°\) (der blaue Winkel). \(F_3\) (der rote Vektor) sei jetzt die Kraft, die das Kräftegleichgewicht herstellt. Die Summe der Kräfte in X- und Y-Richtung ergibt dann
$$F_1 + F_2 \cdot \cos (111°) + F_3 \cdot \cos \alpha = 0$$
$$ F_2 \cdot \sin (111°) + F_3 \cdot \sin \alpha = 0 $$
\(\alpha\) sei der Winkel der Kraft \(F_3\) zur X-Richtung und damit zu \(F_1\). Löst man die Gleichungen nach \(\cos \alpha\) und \(\sin \alpha\) auf, so erhält man für \(\alpha\)
$$\alpha = \arctan\left( \frac{\sin \alpha}{\cos \alpha}\right)= \arctan\left( \frac{- F_2 \cdot \sin (111°)}{-F_1 - F_2 \cdot \cos (111°)}\right) \approx -118,8°$$
und das sind nicht die angegebenen \(129°\) wie auch die Skizze zeigt. Der Betrag der Kraft \(F_3\) berechnet sich z.B. aus der Kräftesumme in Y-Richtung (s.o.).
$$F_3 = \frac{-F_2 \cdot \sin (111°)}{\sin \alpha} \approx 108,7N$$
Gruß Werner