Johannes hat Recht. Die Gewichtskräfte der Balken machen sich in den Lagern quer zur Balkenrichtung bemerkbar.
 Zum einen produziert jeder Balken nur Kräfte in seiner Richtung, da er jeweils drei drehend aufgehängt ist und zum anderen trägt er zusätzlich in jedem Lager die Hälfte seines Gewichtes. Ich unterstelle die Balken sind homogen.
Zum einen produziert jeder Balken nur Kräfte in seiner Richtung, da er jeweils drei drehend aufgehängt ist und zum anderen trägt er zusätzlich in jedem Lager die Hälfte seines Gewichtes. Ich unterstelle die Balken sind homogen.
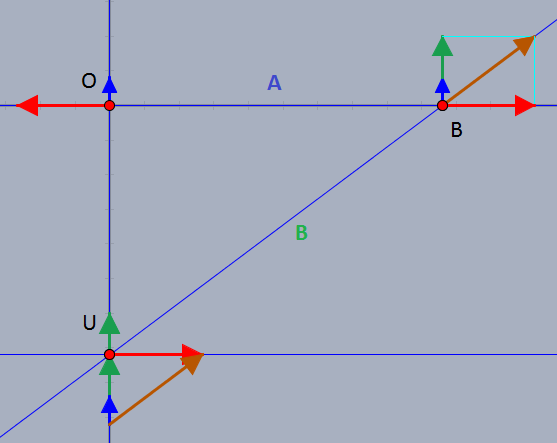
\(O\) sei die Kraft, die das obere Lager auf den Balken \(A\) ausübt. Dann kann man sofort hinschreiben, dass \(O_y=\frac{1}{2}G_A=27\text{kp}\) ist und auf Grund der Kräftegleichheit im Punkt \(B\) gilt
$$\frac{-O_x}{\frac{1}{2}G_A + \frac{1}{2}G_B}=\frac{2,4}{1,8} \quad \Rightarrow O_x=\frac{-2}{3}(G_A+G_B)$$
Die Komponenten der Kraft \(U\), die in dem unteren Lager auf den Balken \(B\) wirken, resultieren dann unmittelbar aus der horizontalen und vertikalen Kräftesumme
$$U_x=-O_x=\frac{2}{3}(G_A+G_B)$$
$$U_y=\frac{1}{2}G_A+G_B$$
Gruß Werner