Aufgabe:
Aufgabe a) ist richtig.
Ich verstehe die Lösung von b) nicht. Könnte mir die jemand erklären? wie soll ich hier mit dem Spannungsteiler rechnen?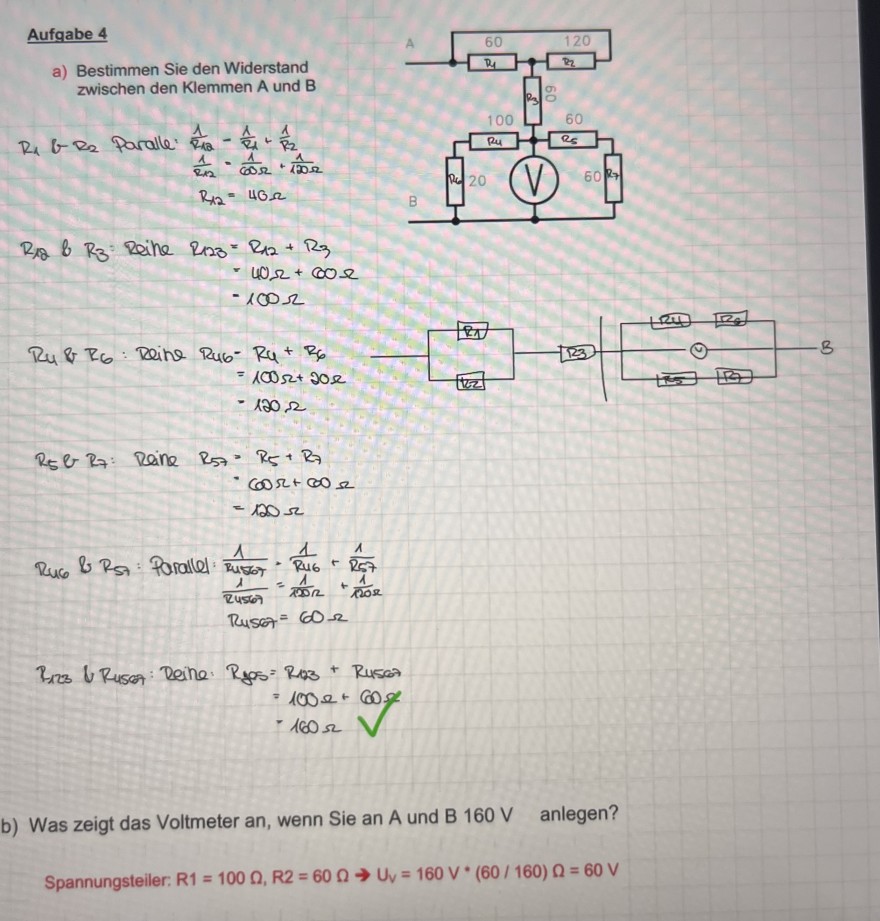
Text erkannt:
Aufgabe 4
a) Bestimmen Sie den Widerstand zwischen den Klemmen A und B
\( \begin{array}{l} R_{1} \& R_{2} \text { paralle } \frac{1}{R / 2}-\frac{1}{R}+\frac{1}{R_{2}} \\ \frac{1}{\varepsilon / 2}=\frac{1}{60 \Omega}+\frac{1}{10 \Omega \Omega} \\ R_{1 / 2}=40 \Omega \end{array} \)
\( \begin{array}{l} R_{12} \text { \& } R_{3} \text { Reike } R_{123}=R_{12}+R_{3} \\ \text { - } 40 \Omega+60 \Omega \\ \text { - } 100 \Omega \end{array} \)
\( \begin{aligned} R_{4} \text { \& } R_{6}: \text { Reine } \begin{aligned} R_{46} & =R_{4}+R_{6} \\ & =100 \Omega+20 \Omega \\ & =120 \Omega \end{aligned} \text {. } \end{aligned} \)
\( \begin{array}{l} R_{5} \text { b } R_{7} \text { : Reine } R_{57}=R_{5}+R_{7} \\ \text { - cosrt } \infty \text { s } \\ =120 \Omega \end{array} \)
\( \begin{array}{l} R_{46} \text { \& } R_{57} \text { : Parallel: } \frac{1}{R_{4}} \frac{1}{107}-\frac{1}{R_{46}}+\frac{1}{R_{57}} \\ \frac{1}{24567}=\frac{1}{1202}+\frac{1}{1202} \\ R_{\text {HSTA }}=60 \Omega \end{array} \)
\( \begin{array}{l} R_{123} \cup R_{4567} \text { : Reine: } R_{y j 5}=R_{123}+R_{4567} \\ =100 \Omega+60 \% \\ \text { - } 160 \Omega \end{array} \)
b) Was zeigt das Voltmeter an, wenn Sie an A und B 160 V anlegen?
Spannungsteiler: \( R 1=100 \Omega, R 2=60 \Omega \rightarrow U_{v}=160 \mathrm{~V} \cdot(60 / 160) \Omega=60 \mathrm{~V} \)