WS15 A1 Strom und Spannungsteiler

Question

Aufgabe:

a) ich verstehe nicht so ganz woher die 30/40 kommen?  Ich weiß das die Stromteiler Regel genutzt wird.

c) Wieso addieren sich die Ströme wenn die Spannungsquelle ausfällt und wenn die Stromquelle ausfällt?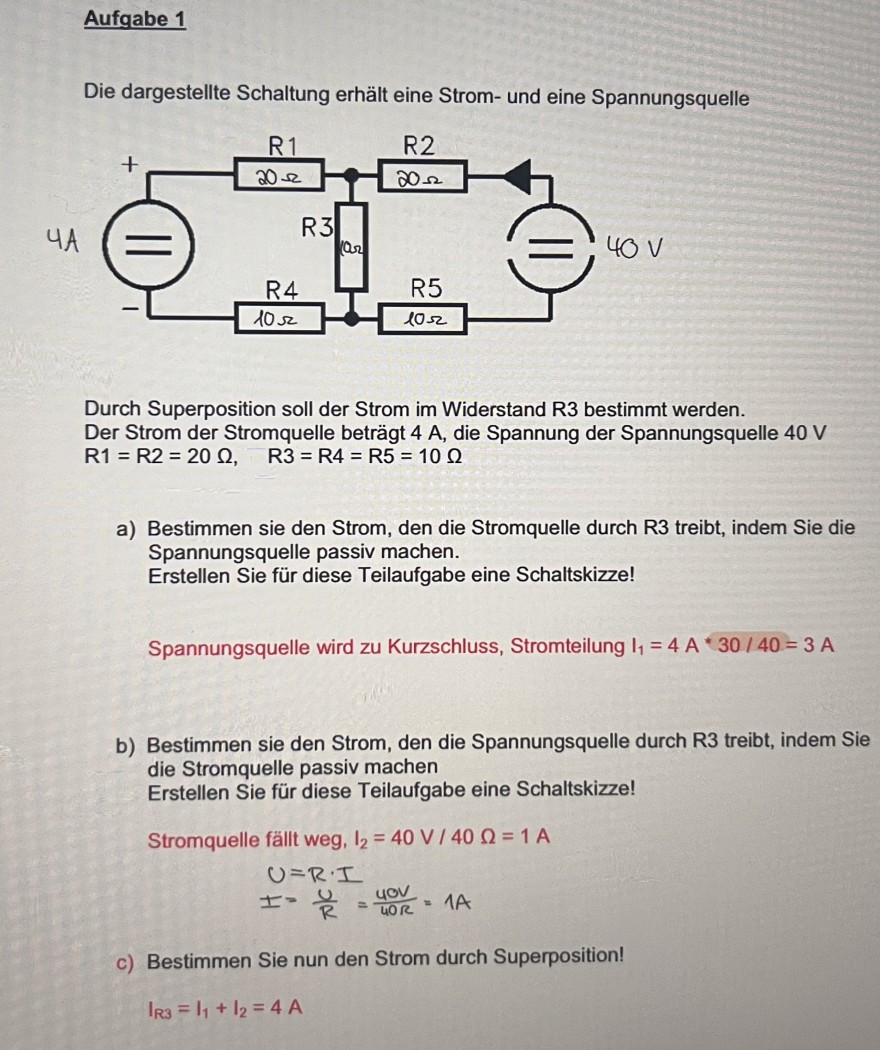

Text erkannt:

Aufgabe 1

Die dargestellte Schaltung erhält eine Strom- und eine Spannungsquelle

Durch Superposition soll der Strom im Widerstand R3 bestimmt werden.
Der Strom der Stromquelle beträgt 4 A , die Spannung der Spannungsquelle 40 V \( \mathrm{R} 1=\mathrm{R} 2=20 \Omega, \quad \mathrm{R} 3=\mathrm{R} 4=\mathrm{R} 5=10 \Omega \)
a) Bestimmen sie den Strom, den die Stromquelle durch R3 treibt, indem Sie die Spannungsquelle passiv machen.
Erstellen Sie für diese Teilaufgabe eine Schaltskizze!

Spannungsquelle wird zu Kurzschluss, Stromteilung \( \mathrm{I}_{1}=4 \mathrm{~A} * 30 / 40=3 \mathrm{~A} \)
b) Bestimmen sie den Strom, den die Spannungsquelle durch R3 treibt, indem Sie die Stromquelle passiv machen
Erstellen Sie für diese Teilaufgabe eine Schaltskizze!
Stromquelle fällt weg, \( \mathrm{I}_{2}=40 \mathrm{~V} / 40 \Omega=1 \mathrm{~A} \)
\( \begin{array}{l} U=R \cdot I \\ I=\frac{U}{R}=\frac{4 O V}{40 R}=1 A \end{array} \)
c) Bestimmen Sie nun den Strom durch Superposition!
\( I_{R 3}=I_{1}+I_{2}=4 \mathrm{~A} \)

Answer 1

hinter R1 teilt sich I auf 30 Ohm nach rechts und 40 nach unten.

lul

Answer 2

Wieso addieren sich die Ströme wenn die Spannungsquelle ausfällt und wenn die Stromquelle ausfällt?

Die Quellen fallen nicht tatsächlich aus, sondern werden nur für dieses Verfahren durch Kurzschluß bzw. Unterbrechung ersetzt. Die Ströme werden addiert, weil das Superpositionsprinzip oder Überlagerungsprinzip dies so vorsieht und weil das zu einem richtigen Gesamtergebnis führt. Die Teilergebnisse sind nur rechnerische Größen und können so nicht gemessen werden.

Comments

Hab’s jetzt so gelöst:

Text erkannt:

Die dargestellte Schaltung erhält eine Strom- und eine Spannungsquelle

Durch Superposition soll der Strom im Widerstand R3 bestimmt werden.
Der Strom der Stromquelle beträgt 4 A , die Spannung der Spannungsquelle 40 V \( R 1=R 2=20 \Omega, \quad R 3=R 4=R 5=10 \Omega \)
a) Bestimmen sie den Strom, den die Stromquelle durch R3 treibt, indem Sie die Spannungsquelle passiv machen.
Erstellen Sie für diese Teilaufgabe eine Schaltskizze!
\( \begin{array}{l} \frac{I_{3}}{I_{9}}=\frac{R_{25}}{R_{25}+R_{3}} \\ I_{3}=I_{9} \cdot \frac{R_{25}}{R_{25}+R_{3}} \\ I_{3}=4 \mathrm{~A} \cdot \frac{8 \Omega \Omega}{30 \Omega+10 \Omega} \\ I_{3 i}=3 \mathrm{~A} \end{array} \)
b) Bestimmen sie den Strom, den die Spannungsquelle durch R3 treibt, indem Sie die Stromquelle passiv machen
Erstellen Sie für diese Teilaufgabe eine Schaltskizze!
durch die
offene
lotrus
flutht in leitung
den orargenen
Bereich Uoin
Strom mehr
\( \begin{aligned} R g \sigma_{0} & =20 \Omega+10 \Omega+10 \Omega \\ & =40 \Omega \\ I= & I z_{2}=\frac{U}{R}=\frac{40 \mathrm{~V}}{40 \Omega}=1 \mathrm{~A} \end{aligned} \)
c) Bestimmen Sie nun den Strom durch Superposition!
\( \begin{aligned} I_{23} & =I_{1}+I_{2}=4 \mathrm{~A} \\ I_{B} & =I_{3 A}+I_{3 A} \\ & -3 \mathrm{~A}+1 \mathrm{~A}=4 \mathrm{~A} \end{aligned} \)