Aufgabe:
Es soll der Arbeitssatz verwendet werden. Was genau ist bei mir falsch? Ich kriege zwar das Ergebnis raus aber mit dem falschen VZ.

Text erkannt:
3.6 Arbeitssatz,
\begin{tabular}{|c|c|}
\hline Aufgabe 3.6.1 Arbeitssatz & "0" "1 \\
\hline \begin{tabular}{l}
Ein Körper der Masse m wird in Position „0" mit der Geschwindigkeit \( \mathrm{v}_{0} \) auf auf eine raue Fläche aufgesetzt. \\
In Position _1" kommt der Körper zum Stillstand. \\
Für alle Kontaktflächen gilt der Gleitreibungsfaktor \( \mu_{G} \). \\
Der Luftwiderstand sei vemachlässigbar.
\end{tabular} & \\
\hline \multicolumn{2}{|l|}{Wie weit rutscht der Körper? Verwenden Sie zur Lösung zwingend den Arbeitssatz! Gegeben: \( \alpha=30^{\circ} \quad \mu_{G}=0,2 \quad g \approx 10 \frac{\mathrm{~m}}{\mathrm{~s}^{2}} \quad v_{0}=5 \frac{\mathrm{~m}}{\mathrm{~s}} \)} \\
\hline \multicolumn{2}{|l|}{\begin{tabular}{l}
Anmerkung: \\
Natürlich kann man die Aufgabe auch über die Dynamische Grundgleichung lösen, dies ist aber hier nicht gefragt. Zu Öbungszwecken kann man dies natürlich zusätzlich tun.
\end{tabular}} \\
\hline
\end{tabular}
Kraft in Wegrichtung \( \rightarrow \) Gleitreibung - entgegen der Bewegung!
\( F_{\text {Wegrichtung }}=-\mu_{G} \cdot N=-\mu_{G} \cdot m \cdot g \)
Arbeitssatz:
\( \begin{array}{c} W_{01}=E_{k i n, 1}-E_{k i n, 0} \\ -\mu_{G} \cdot m \cdot g \cdot \Delta s=0 \quad-\frac{1}{2} \cdot m \cdot v_{1}^{2} \\ \Rightarrow \Delta s=\frac{v_{0}^{2}}{2 \cdot \mu_{G} \cdot g}=6,25 m \end{array} \)
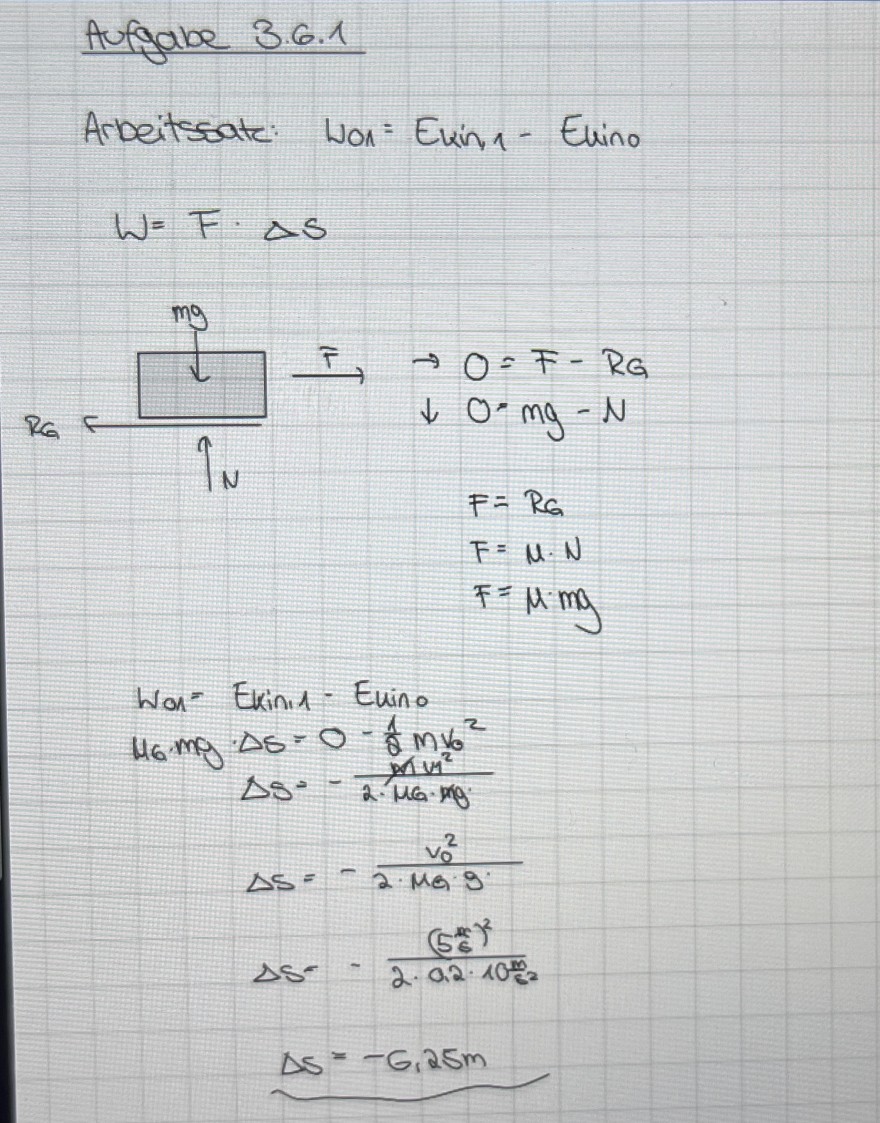
Text erkannt:
Aufgabe 3.6 .1
Arbeitssate: Won = Ekin, - Euino
\( W=F \cdot \Delta S \)
\( \begin{array}{l} \xrightarrow[L]{\mathrm{Ig}} \rightarrow 0=F-R G \\ R_{G} \leftrightarrows \eta_{N} \\ \downarrow \mathrm{O} \cdot \mathrm{mg}-\mathrm{N} \\ F=R_{G} \\ F=\mu \cdot N \\ F=\mu \cdot m g \end{array} \)
\( \begin{array}{l} \text { Wor }=\text { Ekinis-Euino } \\ H_{6} \cdot m g \cdot \Delta s=0-\frac{1}{8} m v^{2} \\ \Delta s=-\frac{\operatorname{mvn}^{2}}{2 \cdot \mu G \cdot P g} \\ \Delta s=-\frac{v_{0}^{2}}{2 \cdot M_{0}} g^{1} \end{array} \)
\( \begin{array}{l} \Delta s=-6,25 m \end{array} \)