Aufgabe:
Es geht um TM.
Für die Flugphase von („1“ nach „2“) wird eine Zeitdauer von ∆t12=0,4 Sekunden gemessen.
c) Skizzieren Sie für die Flugphase von „1“ nach „2“ qualitativ die zeitlichen Verläufe.
• Verwenden Sie dazu die nachfolgenden Diagramme und beschriften Sie diese mit den in der Rechnung
verwendeten Variablen.
• Verwenden Sie dazu zwingend das skizzierte Koordinatensystem
(Tipp: korrekte Vorzeichen und Nullpunkt des Koordinatensystems beachten !)
Wieso beginnt Vy im negativen ?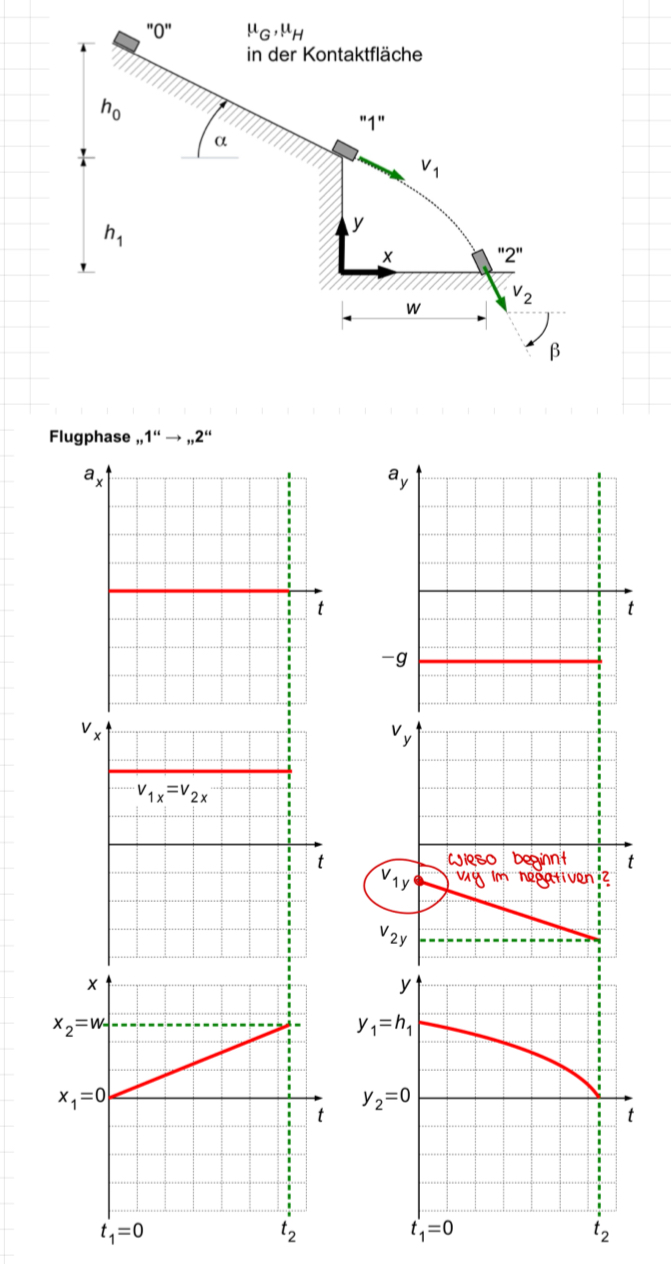
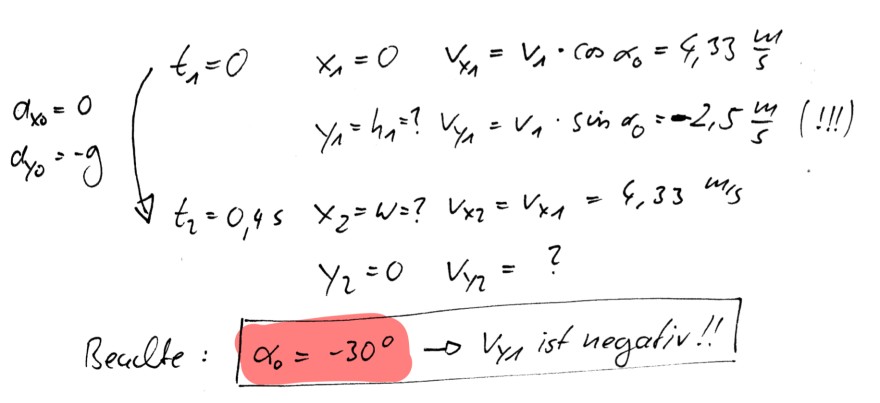
Text erkannt:
\( \begin{array}{ll} a_{x_{0}}=0 \\ d_{y_{0}}=-g \end{array}\left\{\begin{array}{ll} t_{1}=0 & x_{1}=0 \quad v_{x_{1}}=v_{1} \cdot \cos \alpha_{0}=4,33 \frac{\mathrm{~m}}{\mathrm{~s}} \\ & y_{1}=h_{1}=? v_{y_{1}}=v_{1} \cdot \sin \alpha_{0}=-2,5 \frac{\mathrm{~m}}{\mathrm{~s}}(!!!) \\ t_{2}=0,4 \mathrm{~s} & x_{2}=w=? \quad v_{x_{2}}=v_{x_{1}}=4,33 \mathrm{~m} / \mathrm{s} \\ y_{2}=0 & v_{y_{2}}=? \end{array}\right. \)
Bealte: \( \alpha_{0}=-30^{\circ} \rightarrow V_{y_{1}} \) ist negativ!!
Um vy1 und vx1 zu berechnen arbeitet man mit den Winkeln Das verstehe ich alles. Wieso allerdings -30Grad ?