Aufgabe:

Text erkannt:
Es wird eine Anlage zur Befüllung eines Heliumballons betrachtet. Das Helium ( \( \dot{m}=0,01 \mathrm{~kg} / \mathrm{s} \) ) mit einer Temperatur \( \vartheta_{\mathrm{a}}=-10^{\circ} \mathrm{C} \) strömt zunächst durch eine adiabate Drossel, wobei sich der Druck halbiert \( \left(\frac{p_{\mathrm{b}}}{p_{\mathrm{a}}}=0,5\right) \). Danach strömt das Helium durch eine reibungsfreie, nach außen adiabate, elektrisch betriebene Heizvorrichtung HV und zuletzt mit der Temperatur von \( \vartheta_{\mathrm{c}}=40^{\circ} \mathrm{C} \) in den Ballon (siehe Skizze).
Der Ballon besitzt zum Zeitpunkt 0 ein Volumen von \( V_{0}=0,5 \mathrm{~m}^{3} \) und ist mit Helium bei Umgebungsbedingungen gefüllt ( \( p_{0}=p_{\mathrm{U}} \) und \( \vartheta_{0}=\vartheta_{\mathrm{U}} \) ). Er wird für 10 min mit dem Helium (Zustand c) bis zu einem Volumen \( V_{1} \) aufgefüllt, bei dem die Hülle gerade noch ungespannt ist, d. h. der Druck im Ballon dem Umgebungsdruck entspricht \( \left(p_{1}=p_{U}\right) \). Der Wärmeverlust des Heliums über die Ballonhülle zwischen den Zuständen 0 und 1 beträgt \( \left|Q_{\mathrm{V}, 01}\right|=90 \mathrm{~kJ} \).
Nach Erreichen von Zustand 1 strömt weiterhin Helium mit dem gleichen Massenstrom in den Ballon. Unglücklicherweise pickt ein Vogel ein Loch in die Ballonhülle und der Massenstrom \( \dot{m}_{\text {aus }}=\dot{m} \) strömt aus dem Ballon. Nach einer gewissen Zeit stellt sich ein stationärer Zustand 2 mit der Temperatur \( T_{2} \) ein. Der Wärmeverluststrom des Heliums über die Ballonhülle beträgt in diesem Zustand \( \left|\dot{Q}_{\mathrm{V}, 2}\right|=200 \mathrm{~W} \).
Folgende Hinweise sind zu beachten:
- Das Helium kann als ideales Gas mit \( c_{p, \mathrm{He}}=5193 \mathrm{~J} /(\mathrm{kg} \mathrm{K}) \) und \( \kappa_{\mathrm{He}}=1,667 \) angenommen werden.
- Die Umgebungstemperatur beträgt \( \vartheta_{\mathrm{U}}=20^{\circ} \mathrm{C} \) und der Umgebungsdruck \( p_{\mathrm{U}}=1 \) bar.
- Kinetische und potentielle Energien sind zu vernachlässigen.
- Die Rohrleitungen zwischen den Komponenten sind reibungsfrei und adiabat.
- Die Masse der Ballonhülle ist zu vernachlässigen.
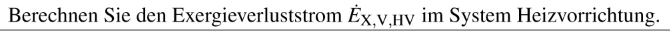
Text erkannt:
Berechnen Sie den Exergieverluststrom \( \dot{E}_{\mathrm{X}, \mathrm{V}, \mathrm{HV}} \) im System Heizvorrichtung.
Ansatz:

Text erkannt:
\( \begin{array}{l}\dot{E}_{\mathrm{X}, \mathrm{V}, \mathrm{HV}}=T_{\mathrm{U}} \cdot \dot{S}_{\mathrm{irr}, \mathrm{bc}} \\ \dot{S}_{\mathrm{c}}-\dot{S}_{\mathrm{b}}=\dot{S}_{\mathrm{Q}}+\dot{S}_{\mathrm{irr}, \mathrm{bc}} \\ \dot{S}_{\mathrm{Qbc}}=0 \quad \text { da adiabat } \\ \dot{S}_{\mathrm{c}}-\dot{S}_{\mathrm{b}}=\dot{m} \cdot\left[c_{p, \mathrm{He}} \cdot \ln \left(\frac{T_{\mathrm{c}}}{T_{\mathrm{b}}}\right)-R_{\mathrm{He}} \cdot \ln \left(\frac{p_{\mathrm{c}}}{p_{\mathrm{b}}}\right)\right] \\ T_{\mathrm{b}}=T_{\mathrm{a}}\end{array} \)
Ich habe zwei Fragen zu der Lösung:
Warum wissen wir, dass pc=pb istbzw. Warum der term=0 ist?
Angenommen der Wärmeübertrager wäre nicht adiabat. Wie würde man dann theoretisch S punkt Q12 berechnen?
Leider hatte ich bis jetzt kein solchen Fall und würde mich deshalb sehr für beide Fragen eine Antwort freuen.
Vielen Dank im voraus