Aufgabe:
Folgende Aufgabe mit folgender Lösung.
Meine Fragen sind folgende:
1) wieso stimmt die Bedingung G+Fqa > Fqb damit das Band nicht umkippt nicht?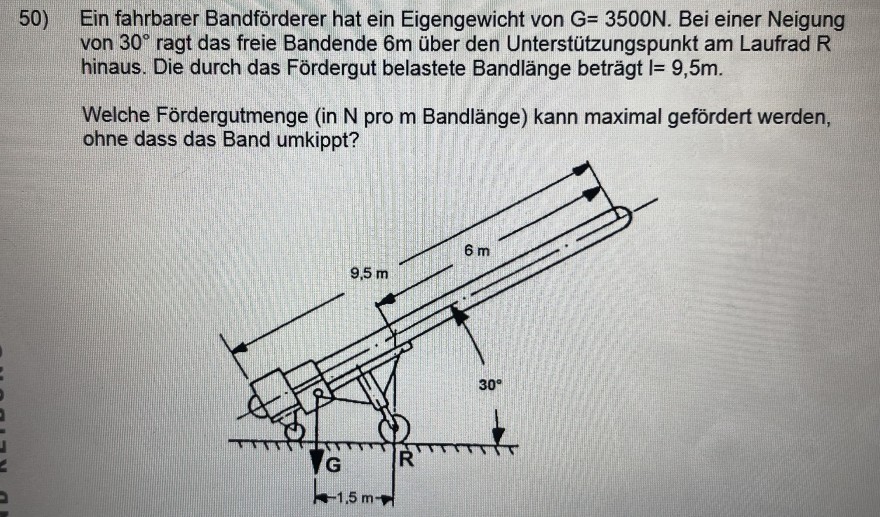
Text erkannt:
50) Ein fahrbarer Bandförderer hat ein Eigengewicht von \( \mathrm{G}=3500 \mathrm{~N} \). Bei einer Neigung von \( 30^{\circ} \) ragt das freie Bandende \( 6 \mathrm{~m} \) über den Unterstützungspunkt am Laufrad \( R \) hinaus. Die durch das Fördergut belastete Bandlänge beträgt \( l=9,5 \mathrm{~m} \).
Welche Fördergutmenge (in \( \mathrm{N} \) pro \( \mathrm{m} \) Bandlänge) kann maximal gefördert werden, ohne dass das Band umkippt?

Text erkannt:
- Das Band kippt, weun das resultierende Moment aller Käfthe im Ulirpigersinn drelst.
- Das Band bleist otehen, wenn das resultierende Moment gegn den Uhitiger dicht.
\( \Rightarrow \) Grente znishen Stekenbleiten and Umpullen: resultierendes Moncent un \( R \cong 0 \)
\( \begin{aligned} \Rightarrow M_{\text {res. }}^{(R)}=0 & =G \cdot 1,5 m+\left[q_{\max }^{*} \cdot a\right] \cdot \frac{q}{2}-\left[q_{\text {max }}^{*} \cdot b\right] \cdot \frac{b}{2} \\ \Leftrightarrow 0 & =G \cdot 1,5 m+q_{\text {max }}^{*} \cdot\left(\frac{a^{2}}{2}-\frac{b^{2}}{2}\right) \end{aligned} \)
\( \Leftrightarrow q_{\max }^{*}=589,5 \frac{\mathrm{N}}{\mathrm{m}} \) : in waagerechter \( x- \) Riclotung gemasen
\( \Rightarrow \) in sandriditimg: \( q_{\text {max }}=\frac{q_{\max }^{*} \cos x}{\cos (2)} q_{\max }=510,5 \frac{\mathrm{N}}{\mathrm{m}} \mathrm{V} \)