Hallo,
Bei einer Kettenlinie ist ganz allgemein$$\frac{F_y}{F_x} = y' \implies (F_y)' = y'' F_x \quad F_x= \text{const}$$ \(F_x\) ist die Kraft in horizontaler und \(F_y\) die in vertikaler Richtung. Das Gewicht \(G=mg\) des Seils pro Länge \(s\) ist im Schwerefeld$$q= \frac{mg}{s}$$mit \(g\) der Erdbeschleunigung und \(m\) dr Masse des Seils. Bei einem Seil, auf das nur die Rotationsbeschleunigung wirkt (Rotation um die X-Achse), ist $$q = \frac{m \omega^2 (-y)}{s}$$Bei einem durchängenden Seil gilt (und sonst auch!), dass die Summe aller vertkalen Kräfte gleich 0 ist, also:$$\text{d}F_y = q \text{d}s = \frac{m \omega^2 (-y)}{s} \text{d}s$$ nach Pythagoras ist$$\text{d}s = \sqrt{(\text{d}x)^2+(\text{d}y)^2} = \sqrt{1+y'^2} \text{d}x $$Einsetzen von \(\text{d}s\)$$\text{d}F_y = \frac{m \omega^2 (-y)}{s} \sqrt{1+y'^2} \text{d}x \\\implies \frac{\text{d}F_y}{\text{d}x} = \left(F_y\right)' = \frac{m \omega^2 (-y)}{s} \sqrt{1+y'^2} = y''F_x$$Die Konstanten fasse ich zu \(k\) zusammen und erhalte dann die DGL$$ y''= -ky\sqrt{1+y'^2}\quad\quad k = \frac{m\omega^2}{sF_x}$$... und dafür habe ich keine Lösung. Zumindest keine analytische Lösung. Ich habe es aber mal grob (mit Excel) nummerisch gerechnet. Und dies sieht so aus:
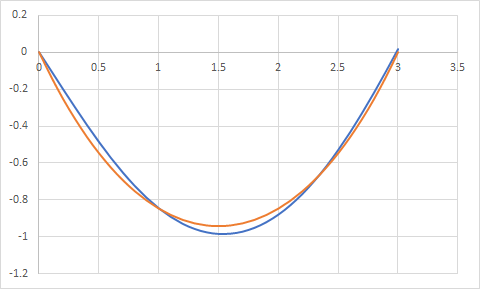
die blaue Kurve ist eine nummerische Lösung obiger DGL. Die orange ist die bekannte Kettenlinie. Wie zu erwarten war, hängt die blaue Kurve mehr durch. D.h. der Teil des Seils, der weiter unten ist und damit weiter von der Rotationsachse entfernt ist, 'zieht' mehr.
Die leichte Asymmetrie ist den Ungenauigkeiten der nummerischen Lösung geschuldet.
Gruß Werner