Aufgabe:
Mathe Quadratische Funktionen
Problem/Ansatz:
Der Faktor a hat für diesen PKW und für eine nasse Straße einen anderen Wert. Gib einen
möglichen Wert für a an und zeichne einen möglichen Bremsgrafen für eine nasse Straße ein.
Begründe deine Entscheidung.
f) Für ein anderes Fahrzeug (Lkw) ergibt sich ein neuer Bremsfaktor a. Bei einer Geschwindigkeit von 60 km
' beträgt der Bremsweg 100 km.
h
Berechne Bremsfaktor a.
g) Stelle für den Lkw den Bremsweg f(x) in Abhängigkeit von der Geschwindigkeit x für den
KM
Bereich 0
< x ≤ 80
grafisch dar.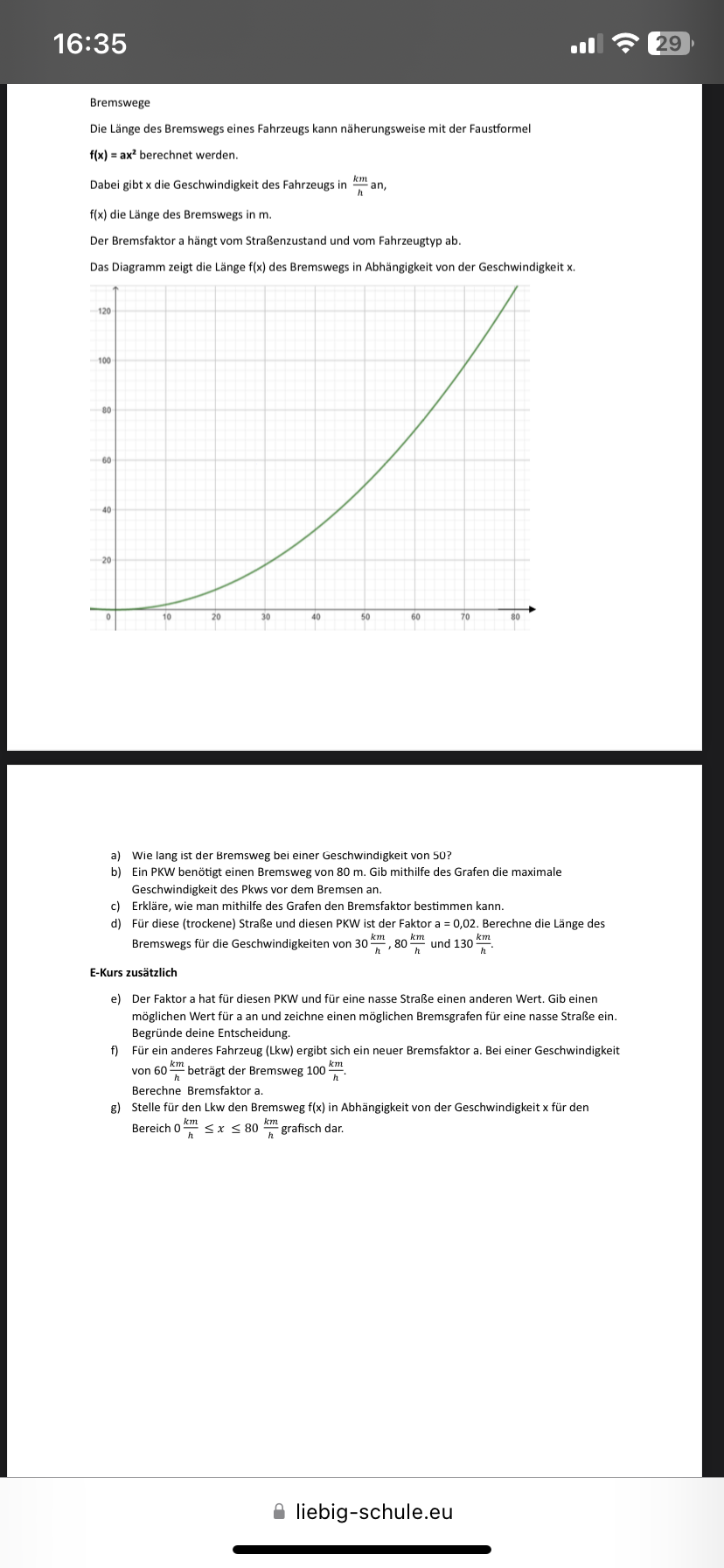
Text erkannt:
\( 16: 35 \)
29
Bremswege
Die Länge des Bremswegs eines Fahrzeugs kann näherungsweise mit der Faustformel \( f(x)=a x^{2} \) berechnet werden .
Dabei gibt \( \mathrm{x} \) die Geschwindigkeit des Fahrzeugs in \( \frac{\mathrm{km}}{\mathrm{h}} \) an,
\( \mathrm{f}(\mathrm{x}) \) die Länge des Bremswegs in \( \mathrm{m} \).
Der Bremsfaktor a hängt vom Straßenzustand und vom Fahrzeugtyp ab.
Das Diagramm zeigt die Länge \( f(x) \) des Bremswegs in Abhängigkeit von der Geschwindigkeit x.
a) Wie lang ist der Bremsweg bei einer Geschwindigkeit von 50 ?
b) Ein PKW benötigt einen Bremsweg von \( 80 \mathrm{~m} \). Gib mithilfe des Grafen die maximale Geschwindigkeit des Pkws vor dem Bremsen an.
c) Erkläre, wie man mithilfe des Grafen den Bremsfaktor bestimmen kann.
d) Für diese (trockene) Straße und diesen PKW ist der Faktor a \( =0,02 \). Berechne die Länge des Bremswegs für die Geschwindigkeiten von \( 30 \frac{\mathrm{km}}{\mathrm{h}}, 80 \frac{\mathrm{km}}{\mathrm{h}} \) und \( 130 \frac{\mathrm{km}}{\mathrm{h}} \).
E-Kurs zusätzlich
e) Der Faktor a hat für diesen PKW und für eine nasse Straße einen anderen Wert. Gib einen möglichen Wert für a an und zeichne einen möglichen Bremsgrafen für eine nasse Straße ein. Begründe deine Entscheidung.
f) Für ein anderes Fahrzeug (Lkw) ergibt sich ein neuer Bremsfaktor a. Bei einer Geschwindigkeit von \( 60 \frac{\mathrm{km}}{\mathrm{h}} \) beträgt der Bremsweg \( 100 \frac{\mathrm{km}}{\mathrm{h}} \). Berechne Bremsfaktor a.
g) Stelle für den Lkw den Bremsweg \( \mathrm{f}(\mathrm{x}) \) in Abhängigkeit von der Geschwindigkeit \( \mathrm{x} \) für den Bereich \( 0 \frac{\mathrm{km}}{\mathrm{h}} \leq x \leq 80 \frac{\mathrm{km}}{\mathrm{h}} \) grafisch dar.
liebig-schule.eu
Text erkannt:
\( 16: 35 \)
29
Bremswege
Die Länge des Bremswegs eines Fahrzeugs kann näherungsweise mit der Faustformel \( f(x)=a x^{2} \) berechnet werden .
Dabei gibt \( \mathrm{x} \) die Geschwindigkeit des Fahrzeugs in \( \frac{\mathrm{km}}{\mathrm{h}} \) an,
\( \mathrm{f}(\mathrm{x}) \) die Länge des Bremswegs in \( \mathrm{m} \).
Der Bremsfaktor a hängt vom Straßenzustand und vom Fahrzeugtyp ab.
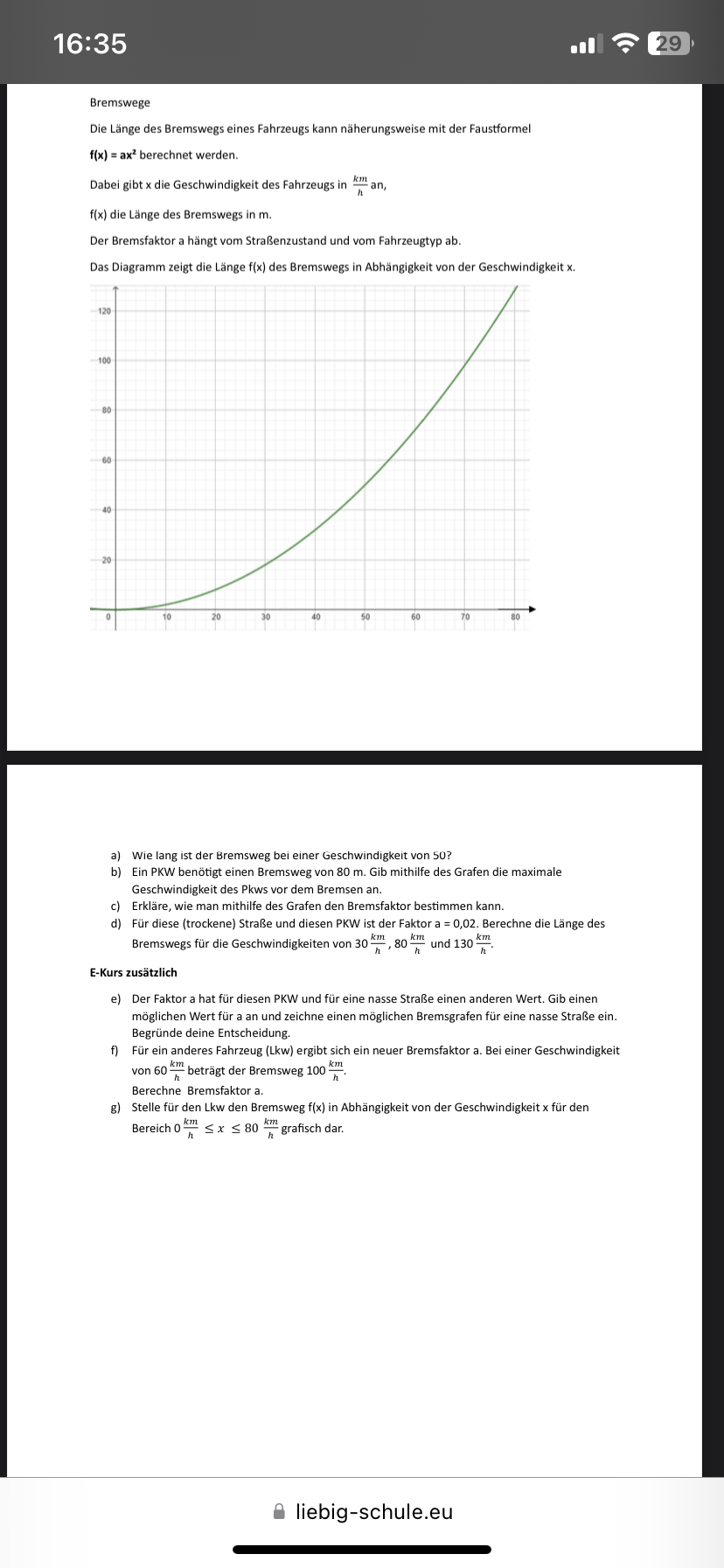
Das Diagramm zeigt die Länge \( f(x) \) des Bremswegs in Abhängigkeit von der Geschwindigkeit x.
a) Wie lang ist der Bremsweg bei einer Geschwindigkeit von 50 ?
b) Ein PKW benötigt einen Bremsweg von \( 80 \mathrm{~m} \). Gib mithilfe des Grafen die maximale Geschwindigkeit des Pkws vor dem Bremsen an.
c) Erkläre, wie man mithilfe des Grafen den Bremsfaktor bestimmen kann.
d) Für diese (trockene) Straße und diesen PKW ist der Faktor a \( =0,02 \). Berechne die Länge des Bremswegs für die Geschwindigkeiten von \( 30 \frac{\mathrm{km}}{\mathrm{h}}, 80 \frac{\mathrm{km}}{\mathrm{h}} \) und \( 130 \frac{\mathrm{km}}{\mathrm{h}} \).
E-Kurs zusätzlich
e) Der Faktor a hat für diesen PKW und für eine nasse Straße einen anderen Wert. Gib einen möglichen Wert für a an und zeichne einen möglichen Bremsgrafen für eine nasse Straße ein. Begründe deine Entscheidung.
f) Für ein anderes Fahrzeug (Lkw) ergibt sich ein neuer Bremsfaktor a. Bei einer Geschwindigkeit von \( 60 \frac{\mathrm{km}}{\mathrm{h}} \) beträgt der Bremsweg \( 100 \frac{\mathrm{km}}{\mathrm{h}} \). Berechne Bremsfaktor a.
g) Stelle für den Lkw den Bremsweg \( \mathrm{f}(\mathrm{x}) \) in Abhängigkeit von der Geschwindigkeit \( \mathrm{x} \) für den Bereich \( 0 \frac{\mathrm{km}}{\mathrm{h}} \leq x \leq 80 \frac{\mathrm{km}}{\mathrm{h}} \) grafisch dar.
liebig-schule.eu