Aufgabe:
habe bzgl einer Arbeitsintegralsaufgabe eine Frage.
Die Aufgabe:
Berechnen Sie die Arbeiten, die an einem Körper verrichtet wird, wenn er die folgenden Wege zurücklegt und worauf die entsprechenden Kräfte wirken:
a) Weg von \( \begin{pmatrix} 1\\1 \end{pmatrix} \) bis zu \( \begin{pmatrix} 4\\8 \end{pmatrix} \) längs der Kurve g(t) = \( \begin{pmatrix} t^2\\t^3 \end{pmatrix} \)
F(x,y) = \( \begin{pmatrix} x^2\\siny \end{pmatrix} \)
Problem/Ansatz:
Wichtige Frage: Wie kommt man auf die Integrationsgrenzen mit denen man später rechnen wird?
Habe es wie folgt versucht, aber das Ergebnis erscheint "unrealistisch".
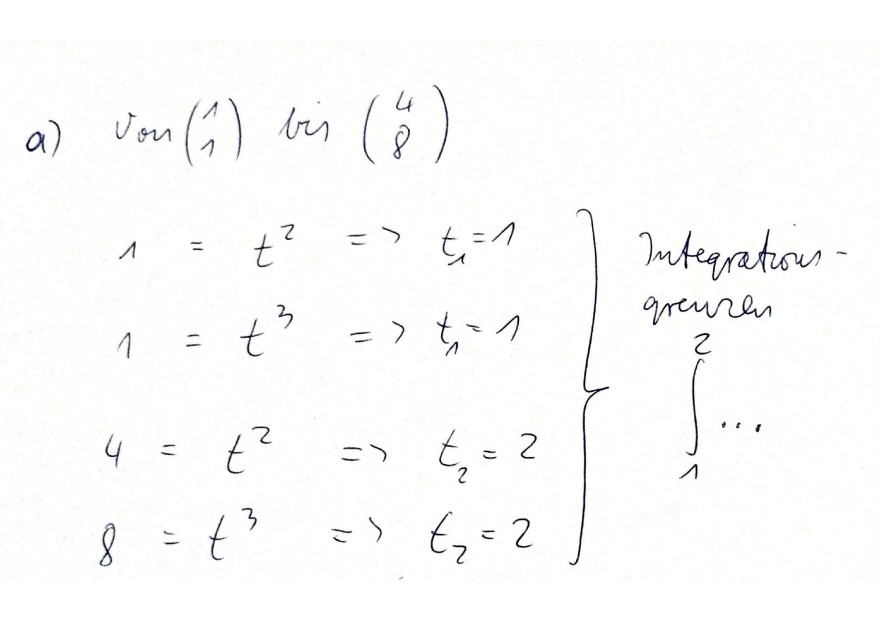
Text erkannt:
a) \( \operatorname{von}\left(\begin{array}{l}1 \\ 1\end{array}\right) \operatorname{bin}\left(\begin{array}{l}4 \\ 8\end{array}\right) \)
\( \left.\begin{array}{l}1=t^{2}=t_{1}=1 \\ 1=t^{3}=>t_{1}=1 \\ 4=t^{2} \Rightarrow t_{2}=2 \\ 8=t^{3} \Rightarrow t_{2}=2\end{array}\right\} \begin{array}{l}\text { Inteqration }- \\ \text { qreuren } \\ 2 \\ \int \limits_{1}^{2} \cdots\end{array} \)