Hallo zusammen, dies hier ist meine Aufgabe, aus dem Fach „Theoretische Elektrotechnik“:
Gegeben ist eine homogene Raumladungsdicht \( \rho_{\mathrm{V}} \) in der Gestalt einer Kugel mit dem Radius \( a \), deren Mittelpunkt im Koordinatenursprung liegt. Der gesamte Raum hat die Permittivität \( \varepsilon \). Berechnen Sie mit Hilfe von der Poisson-Gleichung bzw. Laplace-Gleichung das Potential \( \phi(\vec{r}) \) für den ganzen Raum mit der Randbedingung \( \phi(r=\infty)=0 \).
Die Musterlösung ist
In der Kugel: \( \phi=-\frac{\rho_{\mathrm{V}}}{6 \varepsilon} r^{2}+\frac{\rho_{\mathrm{V}}}{2 \varepsilon} a^{2} \)
Außerhalb: \( \phi=\frac{a^{3} \rho_{\mathrm{V}}}{3 \varepsilon r} \)
Ich löse für den Raum in der Kugel die Poisson-Gleichung:
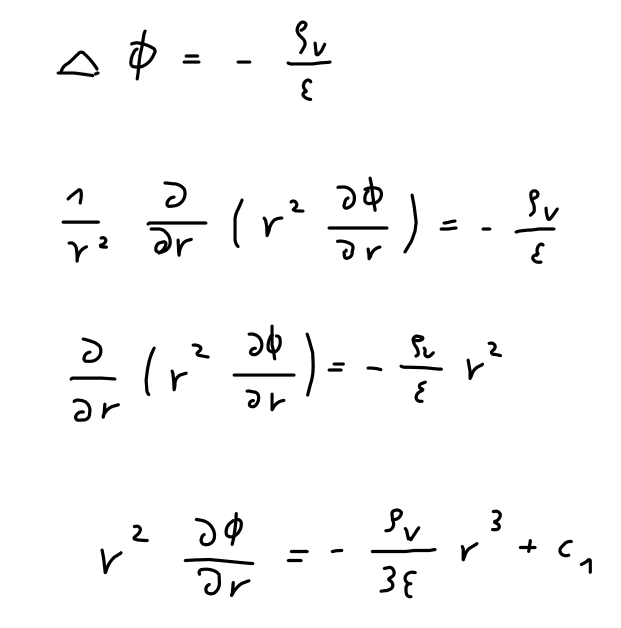
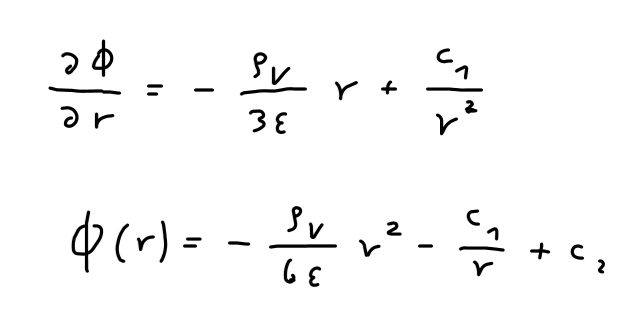
Die Lösung ist:
\( \phi_{i}(r)=-\frac{\rho_{v}}{6 \varepsilon} r^{2}-\frac{c_{1}}{r}+c_{2} \)
Wenn ich für den Raum außerhalb der Kugel die Laplace-Gleichung löse, bekomme ich die Lösung
\( \phi_{a}(r)=-\frac{c_{3}}{r} \)
Mit Hilfe der beiden Gleichungen
\( \phi_{i}(a)=\phi_{a}(a) \quad \) und \( \quad \phi_{i}^{\prime}(a)=\phi_{a}^{\prime}(a) \)
erhalte ich zwei Gleichungen für 3 Unbekannte. Auf die korrekte Lösung komme ich nur, wenn ich c1 = 0 setze. Wieso ist c1 = 0 ?
Vielen Dank!