Hallo MBstudent,
mit dem Standardverfahren zur Berechnung analoger Schaltungen (so, wie es an vielen Hochschulen gelehrt wird) lässt sich die Aufgabe leicht berechnen.
1) Entwicklung des Kleinsignalersatzschaltbildes
Das hast Du ja bereits getan.
2) Aus dem Ersatzschaltbild lassen sich 2 Gleichungen mit 3 Variablen herleiten.
3) Da der Quotient von 2 dieser 3 Variablen gesucht ist, lässt sich das Gleichungssystem lösen und der Kollektorwiderstand \(\large R_{C}\) und anschließen der Kollektorstrom \(\large I_{C}\) berechnen.
Zum Vergleich mit Deiner Berechnung, hier die Ergebnisse:
\(\large R_{C}= 22,689 KΩ\)
\(\large I_{C} = 198,33 µA\)
Falls weitere Infos zur Berechnung benötigt werden, dann einfach fragen.
Gruß von hightech
Hallo,
hier die ausführliche Berechnung mit Kleinsignalersatzschaltbild:
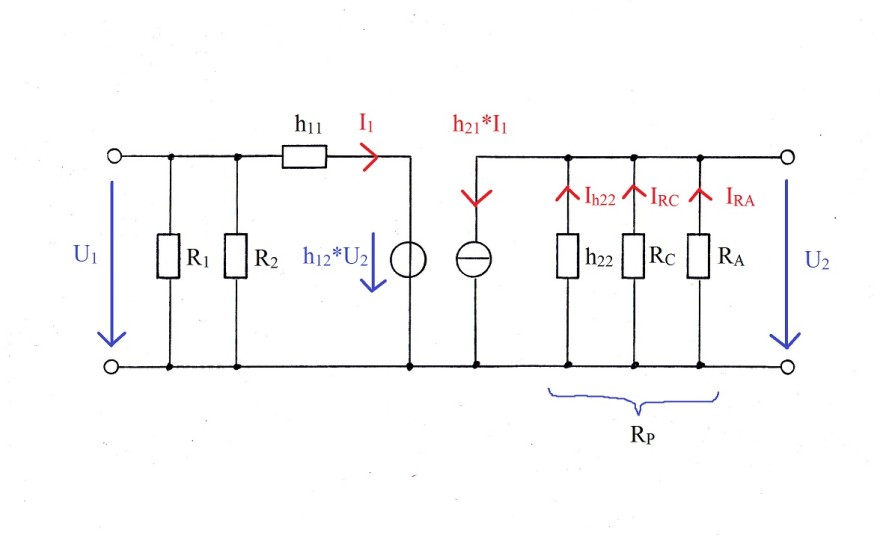
Nachdem du das Kleinsignalersatzschaltbild gezeichnet hast, kommt jetzt die Vierpoltheorie ins Spiel, und zwar die beiden Gleichungen der h-Parameter. Diese lauten:
Gleichung 1: \(\large U_{1} = h_{11}*I_{1} + h_{12}*U_{2}\)
Gleichung 2: \(\large I_{2} = h_{21}*I_{1} + h_{22}*U_{2}\)
Gleichung 1 ist nichts anderes als eine Maschengleichung am Eingang im Kleinsignalersatzschaltbild.
Gleichung 2 ist nichts anderes als eine Knotenpunktgleichung am Ausgang im Ersatzschaltbild, wobei der Strom der Konstantstromquelle auch die Widerstände \(\large R_{C}\) und \(\large R_{A}\) versorgt.
Gleichung 1 kann direkt übernommen werden, also \(\large U_{1} = h_{11}*I_{1} + h_{12}*U_{2}\)
Für \(\large U_{2}\) lässt sich aus dem Ersatzschaltbild ablesen
\(\large U_{2} = - h_{21}*I_{1}*R_{P}\) beachte das negative Vorzeichen, da Spannung und Strom entgegengesetzte Richtung haben. Das bedeutet bezüglich der Spannung \(\large U_{1}\) , dass die Verstärkung negativ ist.
Diese Gleichung nach \(\large I_{1}\) umgestellt
\(\large I_{1} = - \frac{U_{2}}{h_{21}*R_{P}}\) und in Gleichung 1 eingesetzt
\(\large U_{1} = h_{11}*(- \frac{U_{2}}{h_{21}*R_{P}}) + h_{12}*U_{2} = U_{2}*(\frac{h_{12}*h_{21}*R_{P} - h_{11}}{h_{21}*R_{P}})\)
Die Spannungsverstärkung \(\large V_{U}\) ist
\(\large V_{U} = \frac{U_{2}}{U_{1}} = \frac{h_{21}*R_{P}}{h_{11*h_{21}*R_{P} - h_{11}}} = - 75\)
Die Gleichung nach \(\large R_{P}\) aufgelöst und \(\large R_{P}\) ausgerechnet ergibt
\(\large R_{P} = 8612,44Ω\)
Aus \(\large \frac{1}{R_{P}} = h_{22} + \frac{1}{R_{C}} + \frac{1}{R_{A}}\) lässt sich jetzt \(\large R_{C}\) berechnen
\(\large R_{C} = 22,689KΩ\)
Damit wird \(\large I_{C}\)
\(\large I_{C} = \frac{U_{RC}}{R_{C}} = \frac{4,5V}{22,689KΩ}\)
\(\large I_{C} = 198,33µA\)
Gruß von hightech