Hallo,
der Lösungsansatz lautet: Herleitung der Gleichung der Arbeitsgeraden.
Die Gleichung für die Arbeitsgerade lässt sich leicht aus dem Maschenumlauf U0 , URL und UDS herleiten.
\(\large U_{0} - U_{RL} - U_{DS} = 0\)
da \(\large U_{RL} = I_{D}\cdot R_{L}\) und eingesetzt in obige Gleichung, erhält man
\(\large U_{0} - I_{D}\cdot R_{L} - U_{DS}\)
Da das Ausgangskennlinienfeld eine Darstellung \(\large I_{D} = f(U_{DS})\) mit UGS als Parameter ist, muss die Gleichung oben nach \(\large I_{D} = f(U_{DS})\) umgestellt werden
\(\large I_{D} = - \frac{1}{R_{L}}\cdot U_{DS} + \frac{U_{0}}{R_{L}}\) das ist die Gleichung einer Geraden entsprechend \(\large y = a\cdot x + b\)
mit
\(\large a = - \frac{1}{R_{L}}\) und
\(\large b = \frac{U_{0}}{R_{L}}\)
Die Arbeitsgerade lässt sich einzeichnen, indem man die Schnittpunkte der Geraden mit der \(\large I_{D}\)-Achse und der \(\large U_{DS}\)-Achse berechnet:
\(\large I_{D} = 0 + \frac{U_{0}}{R_{L}} = 2,25A\)
\(\large 0 = - \frac{U_{DS}}{R_{L}} + \frac{U_{0}}{R_{L}}\)
\(\large U_{DS} = 9V\)
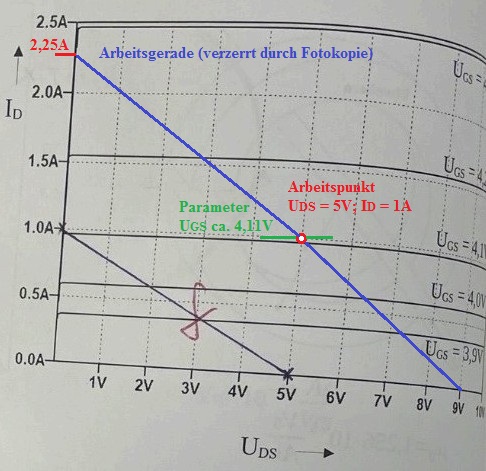
Hier die Arbeitsgerade im Ausgangskennlinienfeld (verzerrt durch die Fotokopie):
Gruß von hightech