Warum wird die Spannungsamplitude kleiner?

Question

Aufgabe:

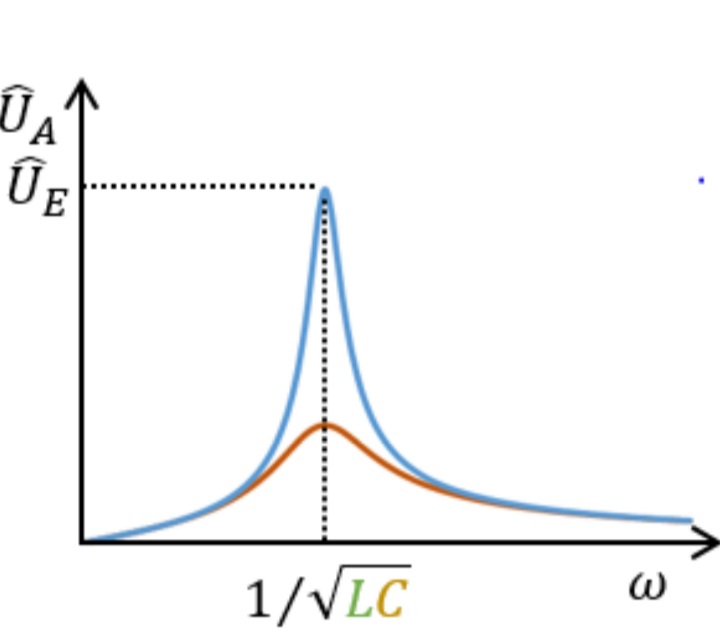
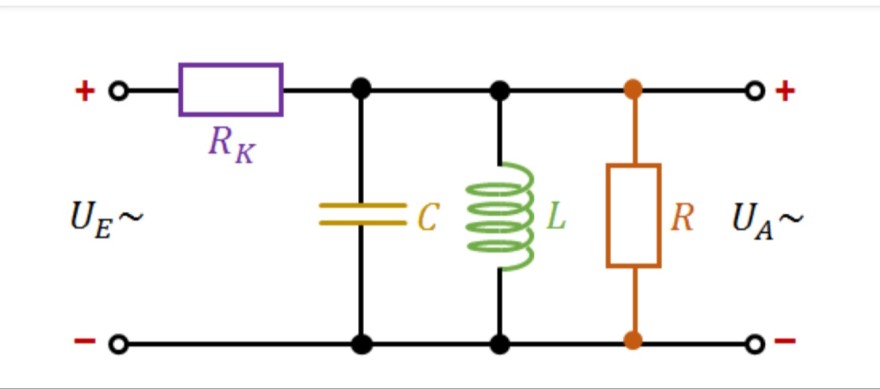
bei einem Parallelschwingkreis wird parallel ein Widerstand R hinzugefügt. Die sich ergebene Resonanzkurve wir nun kleiner, d.h. geringere Spannungsamplitude ( Siehe Anhang ). Halbwertsbreite ist größer.

Problem/Ansatz:

Warum wird die Spannungsamplitude kleiner?

Der Schwingkreis muss irgendwie Energie verlieren. Da der Widerstand R parallel ist, müsste der Schwingkreis Energie verlieren. So. Mit meiner Rechnung komme ich da nicht hinterher.

Bin zu Folgendem gekommen:

Es gilt: 1/RLC + 1/R = 1/R ------->  Der Widerstand dieser beiden ist also R, weil 1/RLC Null ist, da RLC unendlich in Resonanz.

Für den Spannungsteiler ergibt sich : Ue = UR + URk → UR= Ue - URk

Und da ULC und UR parallel sind → ULC = UR , diese Spannung wird letztendlich von Ua gemessen

Problem:

Da UR= Ue - URk gilt bestimmt der Vorwiderstand Rk und nicht R die Spannung die am LC letztendlich anliegt.

Bin mir da total unsicher ob das stimmt, vorallem bei ULC=UR

LG

Answer 1

Hallo

wenn der Widerstand des LC Kreise oo wird hat du die Spannungsteilung zwischen Rk, und R  Dein Ue ist richtig

aber ohne R ist Ue=Ua, also ist Ue nicht nur von Rk abhängig, je kleiner R desto kleiner Ue, U_Rk  ist ja nicht fest, sondern wächst mit fallenden R

irritierend ist deine Schreibweise  RLC  da musste ich erstmal  überlegen, du meinst R an L,C parallel , man würde das als R_L||C schreiben

Comments

Hm. Verstehe gerade nicht warum sich Ue ändert, weil das die angelegte Spannung ist, also vom Experimentator bestimmt.

---

sorry, ich hab a und e verwechselt, also richtig Ua=UR wird umso kleiner, je kleiner R.

---

Cool. Danke für die Hilfe